Leibniz 5.4.2 La elección de horas de trabajo que realiza Ángela
Ángela tiene preferencias cuasilineales respecto al tiempo de trabajo y el grano. En este Leibniz se analizan sus elecciones en tanto que granjera independiente: elige el tiempo de trabajo que maximiza su utilidad, habida cuenta de que la cantidad de grano producido depende, a través de su función de producción, de cuánto trabaja.
Ángela es una agricultora que reparte las horas del día entre el trabajo y el ocio. Su trabajo produce grano, que también consume. Sus horas diarias de ocio se representan como \(t\) y la cantidad de grano que consume diariamente como \(c\). Suponemos que tiene preferencias cuasilineales, representadas, como en el Leibniz 5.4.1, por la función de utilidad:
\[U(t,\ c) = v(t) + c\]donde la función \(v\) es creciente y cóncava. Recuerde que su tasa marginal de sustitución (TMS) es \(v'(t)\).
Supongamos que la cantidad de grano que Ángela puede producir y consumir por día, \(c\), en función de su ocio \(t\) es:
\[c=g(t)\]En otras palabras, se trata de su frontera factible. Es preciso tener en cuenta que la notación ha cambiado un poco respecto a la anterior. Previamente empezábamos con la función de producción \(f(h)\) que relaciona la producción con las horas de trabajo, de manera que la frontera factible se expresaba como \(c=f(24-t)\).
Como la frontera factible debe tener una pendiente descendente, \(g'(t)\lt0\). El valor absoluto de la pendiente de la frontera, o tasa marginal de transformación (TMT), es \(-g'(t)\). Para que la frontera tenga la forma cóncava habitual determinada por los rendimientos marginales decrecientes de las horas de trabajo, es necesario que \(g''(t)\lt0\).
El problema de optimización restringida de Ángela consiste en elegir los valores de \(t\) y \(c\) que maximicen \(v(t) + c\), sujeto a la restricción \(c =g(t)\).
La condición de primer orden para el óptimo puede calcularse aplicando la fórmula habitual \(\text{TMT}=\text{TMS}\) (recuerde el Leibniz 3.5.1) o por sustitución, que en este caso significa elegir \(t\) para maximizar \(v(t) + g(t)\). De uno u otro modo, se obtiene la ecuación:
\[v'(t) + g'(t)=0\]Como \(v''(t)\) y \(g''(t)\) son ambas negativas, la parte izquierda de la ecuación es una función decreciente de \(t\). Se puede deducir que solo existe un valor de \(t\) que satisface esta ecuación. Dicho valor es la elección óptima de ocio de Ángela, que llamaremos \(t^*\). La producción y el consumo óptimos se encuentran, por tanto, en la frontera factible \(c^* = g(t^*)\). Esta asignación óptima se muestra en la figura 1 como el punto P. En esa misma figura, la curva azul es una curva de indiferencia y la curva roja es la frontera factible de Ángela.
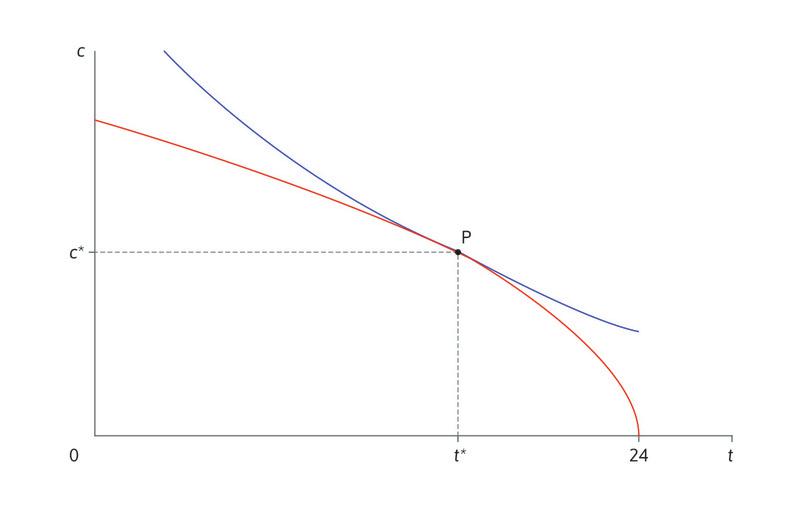
Figura 1 La elección de Ángela entre ocio y grano como agricultora independiente.
Un ejemplo
Ahora pasamos a ilustrar el análisis formal anterior usando funciones específicas de utilidad y producción. Supongamos que en la función de utilidad cuasilineal de Ángela \(U(t,\ c) = v(t) + c\), la función \(v(t)\) es:
\[v(t) = 4\sqrt{t}\]Este es un caso particular del ejemplo de utilidad cuasilineal descrito en el Leibniz 5.4.1: \(U(t,\ c)= b t^\alpha+c\) donde \(b=4\) y \(\alpha= 1/2\).
En segundo lugar, supongamos que la función de producción de Ángela es \(y=2\sqrt{2h}\), donde \(h\) representa las horas de trabajo. Como tiene 24 horas al día para repartir entre trabajo y ocio, \(h + t =24\) y la ecuación de su frontera factible es \(y=g(t)\), donde:
\[g(t) = 2\sqrt{48 -2t}\]Se puede comprobar que esta frontera factible es decreciente (\(g'(t)\lt0\)) y cóncava (\(g''(t)\lt0\)).
Como en el caso anterior, se pueden calcular las tasas marginales de transformación y sustitución a partir de las derivadas de 𝑔 y 𝑣:
\[\text{TMT} = -g'(t) = \frac{2}{\sqrt{48 -2t}}, \quad \text{TMS} = v'(t) = \frac{2}{\sqrt{t}}\]En el óptimo, \(\text{TMT} = \text{TMS}\), de manera que \(48 -2t = t\). Por lo tanto, Ángela elige tener 16 horas diarias de ocio y trabajar durante las 8 horas restantes. A partir de la función de producción, se obtiene que el consumo diario de grano de Ángela es \(2\sqrt{2 \times 8} = 8\).
Puede leer más sobre este tema en las secciones 17.1 a 17.3 de Malcolm Pemberton y Nicholas Rau. (2015) Mathematics for economists: An introductory textbook, (4ª Ed.), Manchester: Manchester University Press.


