Leibniz 5.4.2 Angelan työaikavalinta
Angelalla on kvasilineaariset preferenssit työajan ja viljan välillä. Tässä osiossa tarkastelemme valintoja, joita hän tekee itsenäisenä viljelijänä. Hän valitsee työajan, joka maksimoi hänen saamansa hyödyn. Hänen tuottamansa viljamäärä riippuu tuotantofunktion mukaisesti siitä, miten paljon hän työskentelee.
Angelan päivä jakautuu työaikaan ja vapaa-aikaan. Hän tuottaa viljan ja myös kuluttaa sen. Hänen päivittäinen vapaa-aikansa on \(t\) ja päivittäinen viljankulutuksensa \(c\). Oletamme, että Angelalla on Leibniz-osion 5.4.1 hyötyfunktion mukaiset kvasilineaariset preferenssit:
\[U(t,\ c) = v(t) + c,\]jossa \(v\) on kasvava ja konkaavi funktio. Angelan rajasubstituutiosuhde (MRS) on \(v'(t)\).
Oletetaan, että Angelan päivittäinen viljan tuotanto- ja kulutusmäärä \(c\) riippuu vapaa-ajasta \(t\) seuraavasti:
\[c=g(t).\]Se on toisin sanoen hänen mahdollisuuksien rajansa. Huomaa, että merkintä on hieman erilainen kuin ennen. Aloitimme aikaisemmin tuotantofunktiosta \(f(h)\), joka kuvasi tuotoksen ja työajan suhdetta. Mahdollisuuksien raja esitettiin silloin muodossa \(c=f(24-t)\).
Koska mahdollisuuksien rajan täytyy olla laskeva, \(g'(t)\lt0\). Rajan kulmakertoimen itseisarvo eli rajamuunnossuhde on \(-g'(t)\). Rajalla on tavanomainen konkaavi muoto työajan laskevan rajatuotoksen takia, kun \(g''(t)\lt0\).
Angelan rajoitettu optimointiongelma on valita \(t\) ja \(c\) niin, että \(v(t) + c\) saa maksimiarvonsa, kun otetaan huomioon rajoitus \(c =g(t)\).
Saamme ensimmäisen kertaluvun ehdon optimaaliselle valinnalle tavanomaisella kaavalla \(\text{MRT}=\text{MRS}\) (katso Leibniz 3.5.1) tai sijoittamalla yhtälöstä \(c = g(t)\) hyötyfunktioon, mikä tarkoittaa tässä tapauksessa ajan \(t\) valintaa niin, että \(v(t) + g(t)\) maksimoituu. Päädymme kummallakin tavalla yhtälöön
\[v'(t) + g'(t)=0.\]Koska \(v''(t)\) ja \(g''(t)\) ovat negatiivisia, yhtälön vasen puoli on muuttujan \(t\) vähenevä funktio. Voimme päätellä, että on vain yksi muuttujan \(t\) arvo, joka toteuttaa yhtälön. Se on Angelan optimaalinen vapaa-ajan määrä, \(t^*\). Optimaalinen tuotanto ja kulutus selviävät mahdollisuuksien rajalta: \(c^* = g(t^*)\). Optimaalinen allokaatio on kuvion 1 piste P. Sininen käyrä on samahyötykäyrä ja punainen Angelan mahdollisuuksien raja.
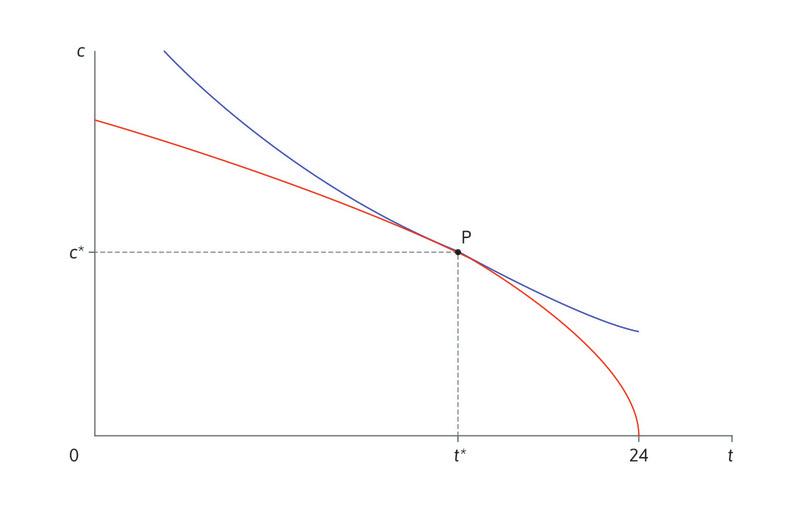
Kuvio 1 Angelan valinta vapaa-ajan ja viljan välillä itsenäisenä viljelijänä.
Esimerkki
Valaisemme analyysia seuraavalla numeerisella esimerkillä. Oletetaan, että Angelan kvasilineaarisessa hyötyfunktiossa \(U(t,\ c) = v(t) + c ,\) funktio \(v(t)\) on
\[v(t) = 4\sqrt{t}.\]Tämä on Leibniz-osiossa 5.4.1 esitetyn kvasilineaarisen hyödyn erikoistapaus: \(U(t,\ c)= b t^\alpha+c\), jossa \(b=4\) ja \(\alpha= 1/2\).
Oletetaan toiseksi, että Angelan tuotantofunktio on \(y=2\sqrt{2h}\), jossa \(h\) on työaika. jos hänellä on \(24\) tuntia päivässä jaettavaksi työn ja vapaa-ajan välillä, \(h + t =24\) ja hänen mahdollisuuksien rajansa on \(y=g(t) ,\) jossa:
\[g(t) = 2\sqrt{48 -2t}\]Voit todistaa, että mahdollisuuksien raja on laskeva (\(g'(t)\lt0\)) ja konkaavi (\(g''(t)\lt0\)).
Rajamuunnossuhteen ja rajasubstituutiosuhteen saa derivoimalla funktiot \(g\) ja \(v\):
\[\text{MRT} = -g'(t) = \frac{2}{\sqrt{48 -2t}}, \quad \text{MRS} = v'(t) = \frac{2}{\sqrt{t}}\]\(\\\\\)Optimaalisessa allokaatiossa \(\text{MRT} = \text{MRS}\), joten \(48 -2t = t\). Siksi Angela valitsee \(16\) tuntia vapaa-aikaa ja \(8\) tuntia työtä. Tuotantofunktiosta voi laskea, että Angelan päivittäinen viljan kulutus on \(2\sqrt{2 \times 8} = 8\) vakkaa.
Lisälukemista: Malcolm Pemberton ja Nicholas Rau. 2015. Mathematics for economists: An introductory textbook, 4. painos (luvut 17.1–17.3). Manchester: Manchester University Press.


