Leibniz 5.8.1 La courbe d’efficacité au sens de Pareto
Il y a beaucoup d’allocations possibles résultant de l’interaction entre Angela et Bruno ; par exemple, nous avons considéré l’allocation qu’imposerait Bruno s’il pouvait utiliser la force, et l’allocation qu’il choisit quand il peut faire une proposition « à prendre ou à laisser » dans un contrat où Angela peut travailler la terre si elle lui paye un loyer sous la forme d’une partie de la production de céréales. Dans ce supplément Leibniz, nous déterminons mathématiquement l’ensemble des allocations qui sont Pareto-efficaces : c’est-à-dire, la courbe d’efficacité au sens de Pareto.
- Pareto-efficace
- Une allocation ayant la propriété qu’il n’y a aucune allocation alternative techniquement possible qui serait plus avantageuse pour au moins une personne sans que quelqu’un d’autre n’en pâtisse.
Une allocation réalisable est Pareto-efficace s’il n’y a pas d’allocation qui la domine au sens de Pareto : c’est-à-dire, il n’est pas possible d’augmenter le bien-être d’une personne sans diminuer celui d’une autre personne. Aussi, afin de trouver une allocation Pareto-efficace entre Bruno et Angela, nous devons commencer par penser à leurs préférences – c’est-à-dire, à ce qui pourrait améliorer leur bien-être.
Angela s’intéresse à son temps libre et aux céréales qu’elle consomme. Elle a une fonction d’utilité quasi-linéaire, et comme dans le Leibniz 5.4.1, nous l’écrivons :
\[U(t,\ c) = v(t) + c\]où \(t\) est son nombre d’heures de temps libre quotidiennes et \(c\) le nombre de boisseaux de céréales qu’elle consomme par jour, et la fonction \(v\) est croissante et concave.
Les préférences de Bruno sont très simples. Il ne s’intéresse qu’à la quantité de céréales qu’il reçoit, que nous désignons par \(R\). Plus \(R\) est élevé, plus Bruno est heureux.
L’ensemble économiquement possible
Nous déterminons ensuite quelles allocations sont économiquement réalisables. La quantité totale de céréales disponibles pour Angela et Bruno est la quantité produite par Angela en utilisant une partie de son temps pour travailler la terre. Comme dans le Leibniz 5.4.1, nous supposons que quand Angela a \(t\) heures de temps libre par jour, elle produit \(g(t)\) boisseaux de céréales. Nous supposons à nouveau que \(g\) est une fonction décroissante et concave : \(g'(t)\lt0\) et \(g''(t)\lt0\).
\(g(t)\) est la quantité de céréales maximale que Bruno et Angela peuvent consommer à eux deux. La frontière des possibles de leur interaction est donc :
\[c+R = g(t)\]Supposez que si Angela ne travaillait pas et recevait des rations de survie de la part de l’État, son niveau d’utilité serait \(u_0\). Elle sera disposée à travailler uniquement si cela lui procure un niveau d’utilité au moins égal à ce niveau. Sa courbe d’indifférence de réserve est :
\[v(t) + c=u_0\]Bruno ne voudra pas participer à l’interaction à moins d’obtenir une quantité de céréales au moins nulle : \(R/geq 0\). (Une quantité négative de céréales impliquerait de donner des céréales de son propre magasin à Angela.)
L’ensemble économiquement possible est l’ensemble d’allocations de céréales pour Angela, \(c\), de céréales pour Bruno, \(R\), et de temps libre pour Angela, \(t\), telles que
\[c+R \leq g(t), R\geq 0 \mbox{ et } v(t) + c \geq u_0\]Ce sont les allocations pour lesquelles la quantité totale de céréales consommée est inférieure ou égale à ce qui est produit, et Angela et Bruno reçoivent tous les deux au moins leur utilité de réserve.
La condition de premier ordre pour des allocations Pareto-efficaces
Une manière de trouver les allocations Pareto-efficaces dans l’interaction entre Angela et Bruno consiste à dire : « Supposez que nous prenions une allocation telle que Bruno reçoive une quantité de céréales \(R\geq 0\). Elle est alors Pareto-efficace si et seulement si Angela est dans la meilleure situation possible, étant donné la quantité de céréales reçue par Bruno, et son utilité est au moins \(u_0\). »
Cela signifie, tout d’abord, que dans une allocation Pareto-efficace, toutes les céréales produites doivent être consommées. Si la quantité de céréales produite est \(g(t)\) et que Bruno consomme \(R\), Angela doit consommer tout le reste : \(c+R = g(t)\). Aucune quantité supplémentaire de céréales n’est laissée de côté.
Deuxièmement, sous la contrainte que toutes les céréales sont consommées, \(c\) et \(t\) doivent ensemble maximiser l’utilité d’Angela. Autrement dit, étant donné \(R\), une allocation \((t,\ c,\ R)\) ne peut être Pareto-efficace que si nous :
\[\text{choisissons }t \text{ et }c \text{ pour maximiser }v(t)+c , \text{ sous la contrainte que }c+R=g(t)\]à condition que cela donne à Angela son utilité de réserve. Ce problème d’optimisation sous contrainte peut être résolu en utilisant d’abord la contrainte pour substituer \(c\). Puisque \(c=g(t)-R\), tout ce que nous devons faire c’est :
\[\text{ choisir }t \text{ pour maximiser }v(t) + g(t) -R\]Ensuite, nous obtenons la condition de premier ordre en dérivant par rapport à \(t\) et en égalisant la dérivée à zéro :
\[v'(t) + g'(t)=0\]Nous avons déjà vu cette équation dans le Leibniz 5.4.2, où nous avions remarqué que l’hypothèse selon laquelle \(v\) et \(g\) sont des fonctions concaves implique qu’elle a au plus une solution. Nous supposons qu’elle existe et la désignons par \(t^*\).
Remarquez que le problème d’optimisation sous contrainte que nous avons résolu est celui qu’Angela résoudrait si Bruno exigeait un loyer égal à \(R\) et qu’elle pouvait choisir \(c\) et \(t\) pour elle-même. La condition de premier ordre est l’équation habituelle \(\text{TMT} = \text{TMS}\), où \(\text{TMT} = -g’(t)\) et \(\text{TMS} = v’(t)\). Dans le supplément Leibniz 5.4.2 nous avons résolu le problème dans le cas où elle était une fermière indépendante : \(R=0\). Nous avons montré ici que son choix de \(t\) serait le même quel que soit le loyer demandé.
Tracer la courbe d’efficacité au sens de Pareto
Nous avons montré que, étant donné la consommation de céréales \(R\) de Bruno, il y a exactement une allocation Pareto-efficace : le temps libre d’Angela est \(t^*\), la solution de la condition de premier ordre :
\[v'(t^*) + g'(t^*)=0\]et sa consommation de céréales est \(g(t^*)-R\). Pour trouver cette allocation, nous avons commencé par fixer un \(R\) arbitraire. En fait, il y a une infinité de valeurs possibles de \(R\), et pour chacune de ces valeurs il y a une allocation Pareto-efficace correspondante.
L’ensemble d’allocations Pareto-efficaces, c’est-à-dire la courbe d’efficacité au sens de Pareto, est l’ensemble de tous les points \((t,\ c,\ R)\) qui satisfont la condition de premier ordre et de toutes les contraintes qui déterminent l’ensemble des combinaisons économiquement possibles. Il est donc donné par les conditions :
\[t=t^*, \quad c+R=g(t^*), \quad c+v(t^*)\geq u_0, \quad R\geq 0\]Dans l’exemple que nous avons vu dans la Figure 5.8 du texte, qui est reproduite et indexée Figure 1 ici, \(t^*=16\). Les allocations Pareto-efficaces sont sur la droite verticale \(t=16\) et la quantité de céréales produites est de \(g(16)=9\) boisseaux. Les points sur cette droite verticale sont les points auxquels le TMS entre temps libre et céréales d’Angela est égal au TMT. Cependant tous les points sur cette ligne ne satisfont pas les autres contraintes. L’ensemble des allocations Pareto-efficaces est compris entre les points C et D. Dans l’allocation représentée par le point G, par exemple, Bruno obtient une quantité de céréales \(R\) donnée par GC, et Angela reçoit le reste.
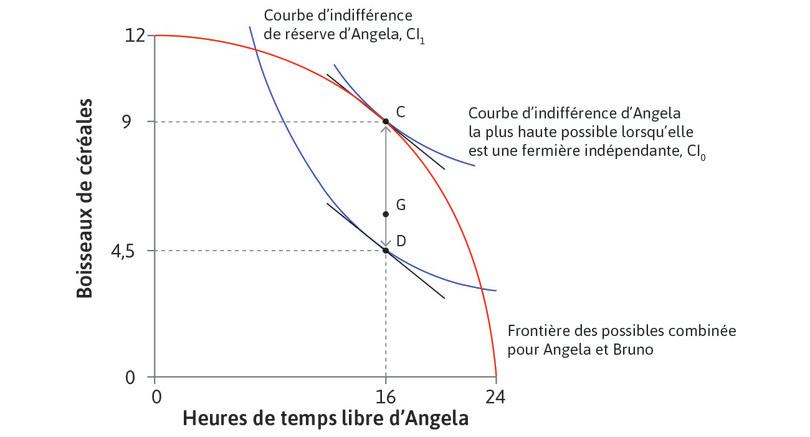
Figure 1 Allocations Pareto-efficaces et la répartition du surplus.
Les allocations avec un \(R\) plus élevé et un \(c\) plus faible sont plus proches de D. Elles bénéficient plus à Bruno et moins à Angela. Les allocations plus proches de C sont meilleures pour Angela et moins bonnes pour Bruno.
Le fait que le temps libre d’Angela soit le même dans toutes les allocations Pareto-efficaces est une conséquence de la quasi-linéarité de ses préférences. Cela ne serait pas le cas si \(U\) prenait une autre forme. Dans d’autres cas, la courbe d’efficacité au sens de Pareto appartiendrait à l’aire en forme ovale de la Figure 1, mais ne serait pas une droite verticale.
La courbe d’efficacité au sens de Pareto : deux exemples
Notre premier exemple illustre les principes des deux sections précédentes en utilisant des fonctions d’utilité et de production spécifiques. Nous donnons ensuite un deuxième exemple dans lequel la fonction d’utilité d’Angela n’est pas quasi-linéaire et la courbe d’efficacité au sens de Pareto est réellement une courbe, et pas une droitee verticale.
1. Fonctions d’utilité et de production spécifiques
Comme dans le Leibniz 5.4.2, nous supposons que la frontière des possibles et la fonction d’utilité d’Angela soient données par :
\[g(t)=2\sqrt{48 -2t}, \quad U(t,\ c) = 4\sqrt{t} + c\]Alors les termes désignés par \(g'(t)\) et \(v'(t)\) ci-dessus sont respectivement :
\[\frac{d}{dt} \left(2(48 -2t)^{1/2}\right) = -2(48 -2t)^{-1/2}, \quad \frac{d}{dt} \left(4t^{1/2}\right) = 2t^{-1/2}\]Ainsi \(t^*\), le nombre d’heures de temps libre quotidiennes d’Angela dans l’allocation Pareto-efficace, est la solution de l’équation :
\[\frac{2}{\sqrt{t}} - \frac{2}{\sqrt{48-2t}} = 0\]Cette équation implique que :
\[t=48-2t\]Par conséquent \(t^*=16\) et la quantité de céréales produite est \(g(t^*)= 2\sqrt{48 -32}=8\). Ainsi dans cet exemple, toute allocation Pareto-efficace doit être telle que :
\[t=16, \quad c+R=8\]De plus, Angela et Bruno doivent tous deux recevoir au moins leur utilité de réserve. L’utilité de réserve d’Angela est atteinte quand elle ne travaille pas (\(t = 24\)) et consomme \(2\) boisseaux de céréales par jour, offerts par l’État. Ainsi son utilité de réserve est \(4\sqrt{24} + 2\). Une allocation Pareto-efficace, avec \(t^*=16\), doit donc satisfaire :
\[4\sqrt{16} +c\geq 4\sqrt{24}+2\]La résolution de cette équation nous donne :
\[c\geq 5,596\]arrondi au millième. La quantité de céréales \(R\) de Bruno doit être au moins nulle. La valeur maximale possible de \(R\) correspond à la quantité qui donne à Angela le moins possible. Puisque \(c+R=8\), c’est \(R=8-5,596=2,404\), arrondi au millième. En résumé, l’intervalle possible pour Bruno est
\[0 \leq R \leq 2,404\]2. Utilité de type Cobb-Douglas
Dans cet exemple, la fonction d’utilité d’Angela est de type Cobb-Douglas :
\[U(t,\ c) = t^{\alpha} c^{1- \alpha}\]où \(0\lt \alpha \lt1\). Pour faciliter les calculs, nous supposons que \(\alpha= \dfrac{8}{13}\). Le taux marginal de substitution (TMS) entre temps libre et céréales d’Angela est donné par la formule habituelle (rappelez-vous le Leibniz 3.4.1) :
\[\text{TMS} = \frac{\partial U}{\partial t} \left/ \frac{\partial U}{\partial c} \right. = \frac{\alpha c}{(1-\alpha)t} = \frac{8c}{5t}\]Soit l’équation de la frontière des possibles \(y=g(t)\). Pour éviter des calculs compliqués, nous supposons que \(g\) a une forme différente de celle du premier exemple :
\[g(t)= \frac{576 - t^2}{40}\]Bien que le graphique de cette fonction ne soit pas le même que celui de la frontière de l’exemple précédent, il a la même forme générale et passe de nouveau à travers les points \((24, 0)\) et \((16, 8)\). Le taux marginal de transformation entre le temps libre d’Angela et sa production de céréales est, comme d’habitude, la valeur absolue de la pente de la frontière des possibles (à pente négative) :
\[\text{TMT} = - g'(t) = \frac{t}{20}\]Étant donnée la rente de Bruno \(R\), la Pareto-efficacité de l’allocation \((t,\ c,\ R)\) nécessite que nous
\(\text{choisissions }t \text{ et }c \text{ pour maximiser }U(t,\ c), \text{ sous la contrainte }g(t) - c =R\).
La condition de premier ordre pour la maximisation, \(\text{TMT} = \text{TMS}\), implique que \(t^2/4 =8c\). En réarrangeant,
\[c=\frac{t^2}{32}\]Les points qui satisfont cette condition dans le quadrant positif du plan \(t-c\) forment une branche de parabole à pente positive. La courbe d’efficacité au sens de Pareto correspond à la section de la courbe qui est économiquement possible.
À l’allocation Pareto-efficace qui est au niveau minimal acceptable pour Bruno, il ne reçoit pas de de loyer et Angela consomme toutes les céréales produites. Par conséquent, à cette allocation,
\[c=\frac{t^2}{32} \, \text{ et } \, c= \frac{576 - t^2}{40}\]En remplaçant la première équation dans la seconde et en multipliant par \(40\), nous voyons que \(5t^2/4 = 576 - t^2\). Donc :
\[t^2 = \frac{-76}{9/4} = 64 \times 4\]Il en découle que \(t = 16\) et \(c = t^2/32 = 8\) : l’allocation Pareto-efficace dans laquelle Bruno ne reçoit pas de céréales (c’est-à-dire qu’Angela ne paye pas de loyer) est la même que dans l’exemple précédent. (Nous avons choisi les nombres pour que cela soit le cas.)
Nous trouvons maintenant l’allocation Pareto-efficace qui est tout juste acceptable pour Angela. Comme dans l’exemple précédent, elle peut obtenir son utilité de réserve en ne travaillant pas et en consommant \(2\) boisseaux de céréales par jour. Ainsi, avec l’allocation Pareto-efficace octroyant à Angela son utilité de réserve,
\[c=\frac{t^2}{32} \, \text{ et } \, t^{\alpha} c^{1- \alpha} = 24^{\alpha} \times 2^{1- \alpha}\]En substituant la première équation dans la deuxième, \(t^{2- \alpha} \! \left/ 32^{1- \alpha} \right. = 24^{\alpha} \times 2^{1- \alpha}\). Par conséquent :
\[t^{2- \alpha} = 24^{\alpha} \times 64^{1- \alpha} = 3^{\alpha} \times 8^{2- \alpha}\]Puisque \(\alpha= \dfrac{8}{13}\), \(\, \dfrac{\alpha}{2- \alpha}= \dfrac{4}{9}\). Ainsi :
\[t = 3^{4/9} \times 8 = 13,036, \quad c = \frac{t^2}{32}= 5,311, \quad y = \frac{576 - t^2}{40}= 10,152\]où tous les nombres sont arrondis au millième. La rente de Bruno \(y-c\) est \(4,841\), arrondie au millième. Puisqu’Angela obtient son utilité de réserve, c’est le loyer le plus élevé pour lequel Angela sera disposée à travailler sur la terre de Bruno.
Pour résumer : dans ce cas la fonction d’utilité d’Angela n’est pas quasi-linéaire. Ses heures de temps libre, et donc ses heures de travail, ne sont pas constantes pour toutes les allocations Pareto-efficaces. La courbe d’efficacité au sens de Pareto dans le plan \(t-c\) n’est pas une droite verticale mais la branche à pente positive de la parabole \(c=t^2/32\) correspondant aux allocations qui sont économiquement possibles. Elle s’étend du point \((13,036,\ 5,311)\) octroyant à Angela son utilité de réserve et à Bruno la rente maximale de \(4,841\) boisseaux par jour, au point \((16,\ 8)\) où Angela consomme toutes les céréales qu’elle produit et Bruno ne reçoit pas de rente.
Pour être sûr(e) d’avoir bien compris cet exemple, essayez de tracer la courbe et comparez-la à celle du cas quasi-linéaire.


