Leibniz 5.4.1 Préférences quasi-linéaires
Angela est une fermière qui veut deux choses : des céréales (qu’elle consomme) et du temps libre. Dans l’Unité 5 nous avons supposé que ses préférences concernant ces deux biens avaient une propriété spéciale : elle valorise les céréales d’un montant constant par rapport au temps libre, indépendamment de la quantité de céréales dont elle dispose déjà. Ce Leibniz montre comment représenter mathématiquement cette propriété.
Dans des Leibniz précédents, nous avons eu beaucoup recours à la fonction d’utilité de type Cobb-Douglas. Nous explorons maintenant une alternative : la fonction d’utilité quasi-linéaire.
Soit \(t\) le nombre d’heures quotidiennes de temps libre d’Angela et c le nombre de boisseaux de céréales qu’elle consomme par jour. Nous supposons, comme dans le texte principal, que le taux auquel Angela est disposée à échanger des céréales contre du temps libre reste constant lorsque sa consommation de céréales augmente. Autrement dit, son taux marginal de substitution entre heures de temps libre et céréales dépend uniquement du temps libre et pas du tout des céréales. Nous avons tracé des courbes d’indifférence avec cette propriété dans la Figure 1 ci-dessus. Pour une quantité de temps libre donnée, disons \(t_0\), la pente de la courbe d’indifférence au point \((t_0,\ c)\) est la même pour tout c, ce qui signifie que dans le graphique les droites tangentes sont parallèles.
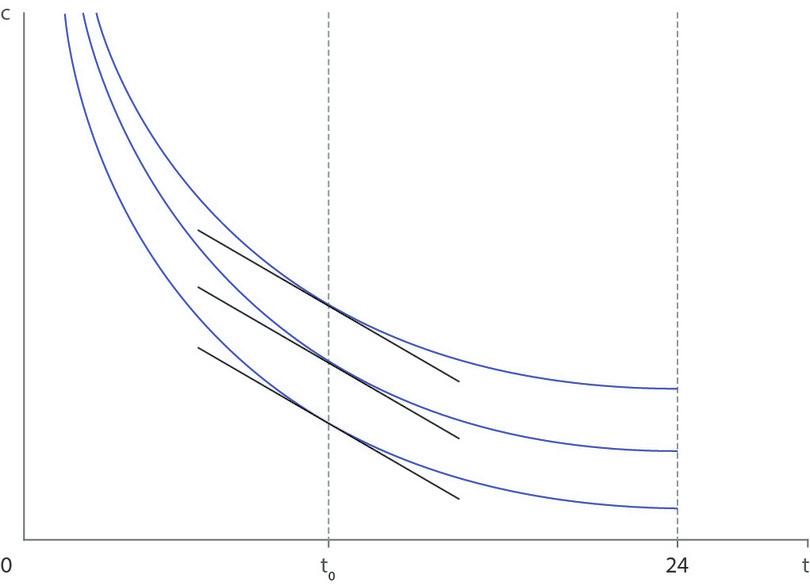
Figure 1 Courbes d’indifférence exhibant la propriété selon laquelle le TMS dépend uniquement du temps libre.
Une fonction d’utilité avec la propriété selon laquelle le taux marginal de substitution (TMS) entre t et c dépend uniquement de t est :
\[U(t,\ c) = v(t) + c\]où \(v\) est une fonction croissante : \(v'(t)\gt0\) car Angela préfère plus de temps libre à moins. Une fonction de ce type est appelée fonction quasi-linéaire parce que l’utilité est linéaire en c et est une fonction de \(t\). Nous montrons maintenant que cette fonction d’utilité a la propriété requise.
Le TMS d’Angela entre le temps libre t et la consommation de céréales c est défini, comme dans le supplément Leibniz 3.2.1, comme la valeur absolue de la pente de la courbe d’indifférence passant par le point \((t,\ c)\). On peut le trouver en utilisant la formule dérivée dans le Leibniz précédent :
\[\text{TMS} = \frac{\partial U}{\partial t} \left/ \frac{\partial U}{\partial c} \right.\]Dans ce cas, \(\dfrac{\partial U}{\partial t}=v'(t)\) et \(\dfrac{\partial U}{\partial c}=1\), donc
\[\text{TMS} = v'(t)\]Le même résultat peut être obtenu directement, sans utiliser la formule générale. Chaque courbe d’indifférence est de la forme :
\[v(t) + c = \text{constante}\]d’où \(c= k - v(t)\), où k est une constante. Par conséquent :
\[\frac{dc}{dt} = - v'(t) \lt0\]le long d’une courbe d’indifférence. La courbe a une pente négative et la valeur absolue de la pente est \(v'(t)\). Ainsi le TMS est une fonction uniquement de t, comme nous voulions le démontrer.
Dans la Figure 1, les courbes d’indifférence ont la propriété habituelle d’un TMS décroissant, puisqu’elles deviennent plus plates lorsque l’on se déplace vers la droite. Pour que cela soit le cas, \(v'(t)\) doit diminuer quand t augmente. Par conséquent \(v''(t)\lt0\) : \(v\) est une fonction concave. Puisque les courbes d’indifférence sont de la forme « \(c = \text{constante} - v(t)\) », deux courbes d’indifférence diffèrent toujours d’une distance verticale constante, comme vous pouvez le voir dans la Figure 1. La raison pour laquelle les courbes du graphique s’entassent horizontalement pour des grandes valeurs de c est simplement qu’elles y sont plus pentues.
Pour résumer : la fonction d’utilité
\[U(t,\ c) = v(t) + c,\]où la fonction \(v\) est croissante et concave, est qualifiée de quasi-linéaire. Le fait d’utiliser une fonction d’utilité de cette forme implique une hypothèse restrictive sur les préférences, mais cela a aussi une propriété très pratique. Puisque l’utilité est de la forme « \(c + \text{quelque chose}\) », elle est mesurée dans les mêmes unités que la consommation. Angela valorise autant ses \(t\) heures de temps libre que \(v(t)\) boisseaux de céréales.
La capacité à mesurer l’utilité en unités de consommation est souvent utile, particulièrement dans les cas où Angela peut vendre ses céréales sur le marché et acheter avec l’argent qui en découle des produits laitiers, des habits ou autres. Dans ce contexte, les économistes interprètent souvent c comme un revenu monétaire. L’hypothèse de préférences quasi-linéaires permet de mesurer les céréales et les pertes d’utilité en termes d’argent.
Un exemple
Un exemple d’une fonction d’utilité quasi-linéaire est :
\[U(t,\ c) = b t^\alpha + c\]où b et \(\alpha\) sont des constantes positives et \(\alpha\lt1\). Vous pouvez voir immédiatement qu’elle est de la forme \(v(t) +c\), avec \(v(t)= b t^\alpha\). Pour démontrer que c’est une fonction d’utilité quasi-linéaire comme décrite ci-dessus, nous devons montrer que la fonction v est croissante et concave. Cela se fait aisément :
\[v'(t)= \alpha b t^{\alpha -1}\]qui est positif puisque \(b\) et \(\alpha\) sont positifs, et :
\[v''(t)= (\alpha -1)\alpha b t^{\alpha -2}\]qui est négatif puisque \(b\gt0\) and \(0\lt\alpha\lt1.\)
Pour en savoir plus : Sections 17.1 à 17.3 de Malcolm Pemberton and Nicholas Rau. 2015. Mathematics for economists: An introductory textbook, 4th ed. Manchester: Manchester University Press.


