Leibniz 5.8.1 Pareto-tehokkuuskäyrä
Angelan ja Brunon vuorovaikutus voi tuottaa monia mahdollisia allokaatioita. Olemme tarkastelleet esimerkiksi Brunon valitsemaa allokaatiota, jos hän voisi pakottaa Angelan työhön, ja toisenlaista allokaatiota, jos Bruno voi tehdä ota tai jätä -tyyppisen tarjouksen ja Angela voisi viljellä maata vain maksamalla Brunolle vuokraa viljana. Tässä Leibniz-osiossa selvitämme matemaattisesti Pareto-tehokkaiden allokaatioiden joukon eli Pareto-tehokkuuskäyrän.
- Pareto-tehokas
- Allokaatio on Pareto-tehokas, jos sille ei ole sellaista teknisesti mahdollista vaihtoehtoa, joka parantaisi ainakin yhden henkilön asemaa huonontamatta kenenkään muun asemaa. Englanniksi pareto efficient.
Mahdollinen allokaatio on Pareto-tehokas, jos sille ei ole sellaista teknisesti mahdollista vaihtoehtoa, joka parantaisi ainakin yhden henkilön asemaa huonontamatta kenenkään muun asemaa. Jos etsimme Pareto-tehokasta allokaatiota Brunon ja Angelan kesken, tarkastelemme ensin heidän preferenssejään ja sitä, mikä parantaisi heidän asemaansa.
Angela arvostaa vapaa-aikaa ja kuluttamaansa viljaa. Hänellä on kvasilineaarinen hyötyfunktio. Kirjoitamme sen samaan muotoon kuin Leibniz-osiossa 5.4.1:
\[U(t,\ c) = v(t) + c,\]jossa \(t\) on Angelan päivittäinen vapaa-aika ja \(c\) hänen päivässä kuluttamansa viljavakkamäärä. Funktio \(v\) on kasvava ja konkaavi.
Brunon preferenssit ovat yksinkertaiset. Hän on kiinnostunut vain saamastaan viljamäärästä \(R\). Brunon asema on sitä parempi, mitä suurempi \(R\) on.
Taloudellisesti mahdolliset allokaatiot
Seuraavaksi selvitämme, mitkä allokaatiot ovat taloudellisesti mahdollisia. Angelan ja Brunon saatavilla oleva kokonaisviljamäärä on määrä, jonka Angela tuottaa käyttämällä osan ajastaan maanviljelyyn. Leibniz-osion 5.4.1 tavoin oletamme, että kun Angelalla on \(t\) tuntia vapaata päivässä, hän tuottaa \(g(t)\) vakkaa viljaa. Oletamme myös, että \(g\) on laskeva ja konkaavi funktio: \(g'(t)\lt0\) and \(g''(t)\lt0\).
\(g(t)\) on suurin viljamäärä, jonka Bruno ja Angela voivat kuluttaa. Heidän vuorovaikutuksensa mahdollisuuksien raja on:
\[c+R = g(t)\]Olettakaamme, että jos Angela ei tekisi työtä ja saisi valtiolta hätäavustuksia, hänen hyötynsä olisi \(u_0\). Hän on halukas työntekoon vain, jos se tuottaa hänelle vähintään yhtä suuren hyödyn. Hänen reservaatio-optionsa samahyötykäyrä on
\[v(t) + c=u_0.\]Bruno ei halua osallistua vuorovaikutukseen, ellei hänen saamansa viljamäärä ole vähintään nolla: \(R\geq0\). (Negatiivinen viljamäärä tarkoittaisi, että Bruno antaisi varastostaan viljaa Angelalle.)
Taloudellisesti mahdolliset allokaatiot ovat niitä, joissa Angela saa viljaa \(c\) ja Bruno \(R\) ja Angelalla on vapaa-aikaa \(t\) tuntia siten, että
\[c+R \leq g(t),\ R\geq 0 \mbox{ ja } v(t) + c \geq u_0.\]Näissä allokaatioissa kulutetun viljan kokonaismäärä on pienempi tai yhtä suuri kuin tuotos ja Angela ja Bruno saavat viljaa vähintään reservaatiohyötynsä verran.
Pareto-tehokkaiden allokaatioiden ensimmäisen kertaluvun ehto
Yksi tapa määrittää Angelan ja Brunon vuorovaikutuksen Pareto-tehokkaat allokaatiot on sanoa: ”Jos Bruno saa viljaa \(R\geq 0\), allokaatio on Pareto-tehokas vain, jos Angelan asema on mahdollisimman hyvä ja hänen hyötynsä on ainakin \(u_0\).”
Tämä tarkoittaa ensinnäkin, että Pareto-tehokkaassa allokaatiossa kaikki tuotettu vilja on myös kulutettava. Jos viljan tuotos on \(g(t)\) ja Bruno kuluttaa \(R\), Angelan on kulutettava loput: \(c+R = g(t)\). Viljaa ei jää lainkaan yli.
Toiseksi määrien \(c\) ja \(t\) summan on yhdessä maksimoitava Angelan hyöty, kun huomioidaan ehto, että kaikki vilja kulutetaan. Toisin sanoen kun \(R\) on annettu, allokaatio \((t,\ c,\ R)\) voi olla Pareto-tehokas vain, jos
\[\text{valitsemme muuttujat }t \text{ ja }c \text{ niin, että }v(t)+c \text{ on mahdollisimman suuri }, \text{ niin että }c+R=g(t),\]kunhan Angela saa reservaatiohyödyn. Rajoitetun optimointiongelman voi ratkaista ratkaisemalla muuttujan \(c\) rajoitteesta \(c + R = g(t)\). Koska \(c=g(t)-R\), meidän on vain
\[\text{valittava }t \text{ niin, että }v(t) + g(t) -R \text{ on mahdollisimman suuri. }\]Derivoimalla muuttujan \(t\) suhteen ja asettamalla derivaatan nollaksi saamme ensimmäisen kertaluvun ehdon
\[v'(t) + g'(t)=0.\]Näimme saman yhtälön Leibniz-osiossa 5.4.2. Se, että \(v\) ja \(g\) ovat konkaaveja funktioita, tarkoittaa, että yhtälöllä on enintään yksi ratkaisu. Oletamme, että ratkaisu on olemassa ja merkitsemme sitä \(t^*\).
Huomaa, että ratkaisemamme rajoitettu optimointiongelma koskisi Angelaa, jos Bruno vaatisi häneltä vuokraa \(R\) ja hän valitsisi itse muuttujat \(c\) ja \(t\). Ensimmäisen kertaluvun ehto on tuttu yhtälö \(\text{MRT} = \text{MRS}\), missä \(\text{MRT} = -g’(t)\) ja \(\text{MRS} = v’(t)\). Leibniz-osiossa 5.4.2 ratkaisimme ongelman siinä tapauksessa, että Angela oli itsenäinen viljelijä: \(R=0\). Olemme osoittaneet nyt, että hänen valintansa \(t\) olisi sama riippumatta vaaditun vuokran määrästä.
Pareto-tehokkuuskäyrän piirtäminen
Olemme osoittaneet, että kun Bruno kuluttaa viljaa määrän \(R\), on vain yksi Pareto-tehokas allokaatio: Angelan vapaa-ajan määrä on \(t^*,\) ensimmäisen kertaluvun ehdon ratkaisu:
\[v'(t^*) + g'(t^*)=0\]ja hän kuluttaa viljaa \(g(t^*)-R\). Aloitimme allokaation selvittämisen antamalla keinotekoisen arvon muuttujalle \(R\). Todellisuudessa muuttujalle \(R\) on loputon määrä mahdollisia arvoja, ja jokaiselle niistä on vastaava Pareto-tehokas allokaatio.
Kaikkien Pareto-tehokkaiden allokaatioiden joukko eli Pareto-tehokkuuskäyrä on kaikkien niiden pisteiden \((t,\ c,\ R)\) joukko, joka toteuttaa ensimmäisen kertaluvun ehdon ja kaikki taloudellisesti mahdollisen joukon ehdot. Sen siis määrittävät seuraavat ehdot:
\[t=t^*, \quad c+R=g(t^*), \quad c+v(t^*)\geq u_0, \quad R\geq 0\]Näkemässämme esimerkissä kuviossa 5.8, joka on myös tässä kuviona 1, \(t^*=16\). Pareto-tehokkaat allokaatiot ovat pystysuoralla viivalla \(t=16\), ja viljan tuotantomäärä on \(g(16)=9\) vakkaa. Pystysuoran viivan pisteissä Angelan vapaa-ajan ja viljan rajasubstituutiosuhde on yhtä suuri kuin rajamuunnossuhde. Kaikki pisteet eivät kuitenkaan täytä muita ehtoja. Kaikkien Pareto-tehokkaiden allokaatioiden joukko sijoittuu pisteiden C ja D väliin. Esimerkiksi pisteen G allokaatiossa Bruno saa viljaa janan GC ilmoittaman määrän \(R\) ja Angela saa loput.
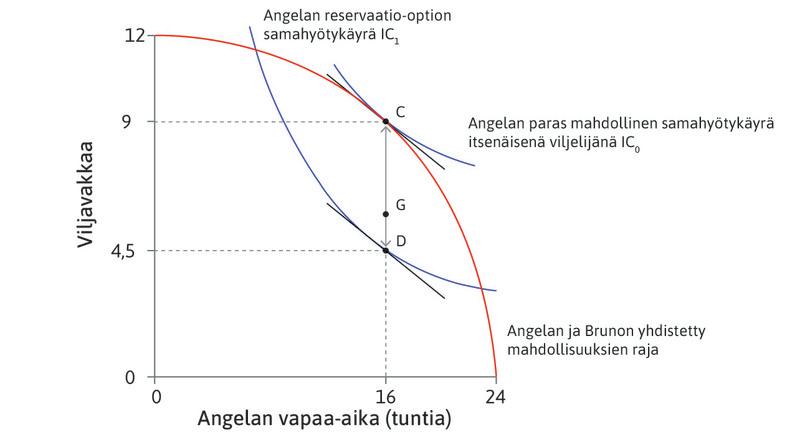
Kuvio 1 Pareto-tehokkaat allokaatiot ja ylijäämän jakautuminen.
Allokaatiot, joissa on suurempi \(R\) ja pienempi \(c\), ovat lähempänä pistettä D. Niistä on enemmän hyötyä Brunolle ja vähemmän Angelalle. Lähempänä pistettä C olevat allokaatiot ovat parempia Angelalle ja huonompia Brunolle.
Angelan vapaa-aika on sama kaikissa Pareto-tehokkaissa allokaatioissa, mikä seuraa siitä, että hänellä on kvasilineaarinen hyötyfunktio. Tulos ei pätisi muille hyödyn \(U\) muodoille. Muissa tapauksissa Pareto-tehokkuuskäyrä olisi kuvion 1 linssinmuotoisella alueella muttei olisi pystysuora viiva.
Kaksi esimerkkiä Pareto-tehokkuuskäyrästä
Ensimmäinen esimerkkimme valaisee kahden aikaisemman alaluvun periaatteita tietyillä hyöty- ja tuotantofunktioilla. Jälkimmäisessä esimerkissä Angelan hyötyfunktio ei ole kvasilineaarinen ja Pareto-tehokkuuskäyrä on oikeasti käyrä eikä pystysuora viiva.
1. Hyöty- ja tuotantofunktiot
Oletamme Leibniz-osion 5.4.2 tavoin, että mahdollisuuksien raja ja Angelan hyötyfunktio saadaan seuraavasti:
\[g(t)=2\sqrt{48 -2t}, \quad U(t,\ c) = 4\sqrt{t} + c\]Termit \(g'(t)\) ja \(v'(t)\), ovat
\[\frac{d}{dt} \left(2(48 -2t)^{1/2}\right) = -2(48 -2t)^{-1/2}, \quad \frac{d}{dt} \left(4t^{1/2}\right) = 2t^{-1/2}.\]Angelan päivittäinen vapaa-aika jokaisessa Pareto-tehokkaassa allokaatiossa, \(t^*\), ratkaisee yhtälön
\[\frac{2}{\sqrt{t}} - \frac{2}{\sqrt{48-2t}} = 0.\]Yhtälö toteutuu, kun
\[t=48-2t.\]Siksi \(t^*=16\) ja viljan tuotantomäärä on \(g(t^*)= 2\sqrt{48 -32}=8\). Tässä esimerkissä jokaisen Pareto-tehokkaan allokaation \((t,\ c,\ R)\) tulee täyttää ehdot
\[t=16, \quad c+R=8.\]Lisäksi Angelan ja Brunon täytyy saada vähintään reservaatiohyötynsä verran. Angelan reservaatiohyöty toteutuu, kun hän ei tee työtä ollenkaan \((t = 24)\) ja kuluttaa \(2\) valtion toimittamaa viljavakkaa päivässä. Hänen reservaatiohyötynsä on siis \(4\sqrt{24} + 2\). Pareto-tehokkaan allokaation, jossa \(t^*=16\), tulee täyttää ehto
\[4\sqrt{16} +c\geq 4\sqrt{24}+2\]Epäyhtälön ratkaisemalla saamme
\[c\geq 5~596\]kolmen desimaalin tarkkuudella. Brunon viljamäärän \(R\) on oltava vähintään nolla. Muuttujan \(R\) mahdollinen maksimiarvo on määrä, joka antaa Angelalle mahdollisimman vähän. Koska \(c+R=8\), se on \(R=8-5~596=2~404\) kolmen desimaalin tarkkuudella. Brunolle mahdollisten arvojen joukko on
\[0 \leq R \leq 2~404.\]2. Cobb–Douglas-hyötyfunktio
Tässä esimerkissä Angelan hyötyfunktio on Cobb–Douglas-muotoa:
\[U(t,\ c) = t^{\alpha} c^{1- \alpha},\]jossa \(0\lt \alpha \lt1\). Jotta lukuja on helpompi käsitellä, oletamme, että \(\alpha= \dfrac{8}{13}\). Angelan vapaa-ajan ja viljan kulutuksen rajasubstituutiosuhde käy ilmi tutusta kaavasta (katso Leibniz 3.4.1):
\[\text{MRS} = \frac{\partial U}{\partial t} \left/ \frac{\partial U}{\partial c} \right. = \frac{\alpha c}{(1-\alpha)t} = \frac{8c}{5t}\]Olkoon mahdollisuuksien rajan yhtälö \(y=g(t)\). Mutkikkailta laskutoimituksista välttyäksemme oletamme, että \(g\) on muodoltaan erilainen kuin ensimmäisessä esimerkissä:
\[g(t)= \frac{576 - t^2}{40}\]Vaikka funktion kuvaaja ei ole sama kuin edellisen esimerkin mahdollisuuksien raja, se on laadullisilta ominaisuuksiltaan samankaltainen ja kulkee nytkin pisteiden \((24, 0)\) ja \((16, 8)\) kautta. Angelan vapaa-ajan ja viljan tuotannon rajamuunnossuhde on (laskevan) mahdollisuuksien rajan kulmakertoimen itseisarvo:
\[\text{MRT} = - g'(t) = \frac{t}{20}\]Kun Brunon vuokra on \(R\), allokaation \((t,\ c,\ R)\) Pareto-tehokkuus vaatii, että
\[\text{valitsemme muuttujat }t \text{ ja }c \text{ niin, että }U(t,\ c), \text{ on mahdollisimman suuri, kun huomioidaan ehto }g(t) - c =R.\]Ensimmäisen kertaluvun ehto maksimille, \(\text{MRT} = \text{MRS}\), tarkoittaa, että \(t^2/4 =8c\). Järjestellään termit:
\[c=\frac{t^2}{32}\]Pisteet, jotka toteuttavat tämän yhtälön, muodostavat ylöspäin aukeavan paraabelin kasvavan puolikkaan. Pareto-tehokkuuskäyrä on käyrän taloudellisesti mahdollinen osa.
Pareto-tehokkaassa allokaatiossa, jonka Bruno juuri ja juuri hyväksyy, hän ei saa vuokraa ja Angela kuluttaa kaiken tuottamansa viljan. Siinä allokaatiossa
\[c=\frac{t^2}{32} \, \text{ ja } \, c= \frac{576 - t^2}{40}.\]Sijoittamalla ensimmäisen yhtälön toiseen ja kertomalla arvolla \(40\) näemme, että \(5t^2/4 = 576 - t^2\). Siten
\[t^2 = \frac{-76}{9/4} = 64 \times 4\]Siitä seuraa, että \(t = 16\) ja \(c = t^2/32 = 8\): Pareto-tehokas allokaatio, jossa Bruno ei saa viljaa (eli Angela ei maksa vuokraa), on sama kuin edellisessä esimerkissä. (Valitsimme luvut niin, että näin käy.)
Nyt ratkaisemme Pareto-tehokkaan allokaation, jonka Angela voi juuri ja juuri hyväksyä. Edellisen esimerkin tapaan hän voi saada reservaatiohyödyn tekemättä ollenkaan työtä ja kuluttamalla \(2\) vakkaa viljaa päivässä. Pareto-tehokkaassa allokaatiossa, jossa Angela saa reservaatiohyödyn,
\[c=\frac{t^2}{32} \, \text{ ja } \, t^{\alpha} c^{1- \alpha} = 24^{\alpha} \times 2^{1- \alpha}.\]Sijoitamme ensimmäisen yhtälön toiseen, \(t^{2- \alpha} \! \left/ 32^{1- \alpha} \right. = 24^{\alpha} \times 2^{1- \alpha}\). Siten
\[t^{2- \alpha} = 24^{\alpha} \times 64^{1- \alpha} = 3^{\alpha} \times 8^{2- \alpha}.\]Koska \(\alpha= \dfrac{8}{13}\), \(\, \dfrac{\alpha}{2- \alpha}= \dfrac{4}{9}\). Siksi:
\[t = 3^{4/9} \times 8 = 13,036, \quad c = \frac{t^2}{32}= 5,311, \quad y = \frac{576 - t^2}{40}= 10~152,\]kaikki kolmen desimaalin tarkkuudella. Brunon vuokra \(y-c\) on \(4~841\) kolmen desimaalin tarkkuudella. Koska Angela saa reservaatiohyötynsä, tämä on suurin vuokra, jolla Angela on halukas työskentelemään Brunon maalla.
Yhteenvetona: tässä tapauksessa Angelan hyötyfunktio ei ole kvasilineaarinen. Hänen vapaa-aikansa ja työaikansa eivät ole vakioita kaikissa Pareto-tehokkaissa allokaatioissa. \(t-c\) -tasoon piirretty Pareto-tehokkuuskäyrä ei ole pystysuora vaan taloudellisesti mahdollisia allokaatioita vastaavan ylöspäin aukeavan paraabelin \(c=t^2/32\) osa. Se lähtee pisteestä \((13~036,\ 5~311)\), jossa Angela saa reservaatiohyötynsä ja Bruno saa maksimivuokran \(4~841\) vakkaa päivässä, ja päättyy pisteeseen \((16,\ 8)\), jossa Angela kuluttaa kaiken tuottamansa viljan ja Bruno ei saa vuokraa.
Voit varmistaa esimerkin ymmärtämisen piirtämällä käyrän ja vertaamalla sitä kvasilineaarisen tapauksen käyrään.


