Leibniz 5.4.1 Kvasilineaariset preferenssit
Angela on viljelijä, joka tekee valinnan kahden hyödykkeen, viljan ja vapaa-ajan, välillä. Oletamme Angelan preferenssit tässä luvussa sellaisiksi, että lisäyksikkö viljaa vastaa hänelle samaa vapaa-ajan määrää riippumatta siitä, kuinka paljon hänellä on viljaa. Tässä osiossa esitämme tämän ominaisuuden matemaattisesti.
Aikaisemmissa Leibniz-osioissa olemme käyttäneet Cobb–Douglas-tuotantofunktiota. Nyt tutkimme vaihtoehtoista keinoa: kvasilineaarista hyötyfunktiota.
Kuvatkoon muuttuja \(t\) Angelan päivittäistä vapaa-aikaa ja \(c\) hänen päivässä kuluttamaansa viljamäärää. Oletamme, että vaihtosuhde, jolla Angela on valmis vaihtamaan viljaa vapaa-ajaksi, pysyy viljan kulutuksen kasvaessa vakiona. Toisin sanoen hänen vapaa-ajan ja viljavakkojen rajasubstituutiosuhteensa riippuu vain vapaa-ajasta eikä lainkaan viljasta. Kuvioon 1 on hahmoteltu tällaisia samahyötykäyriä. Jos vapaa-aikaa on \(t_0\), samahyötykäyrän kulmakerroin hetkenä \((t_0,\ c)\) on sama kaikilla muuttujan \(c\) arvoilla. Kaikki kuvion tangenttisuorat ovat siis yhdensuuntaisia.
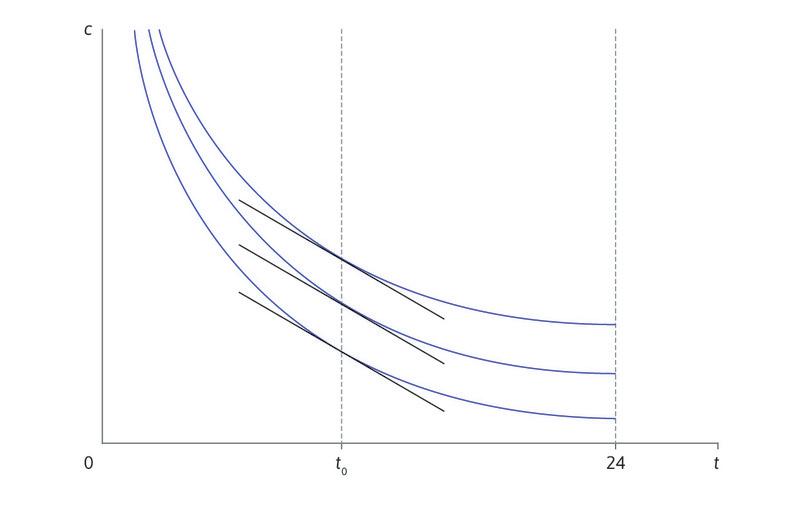
Kuvio 1 Samahyötykäyrät, kun rajasubstituutiosuhde riippuu vain vapaa-ajasta.
Jos muuttujien \(t\) ja \(c\) rajasubstituutiosuhde riippuu vain muuttujasta \(t\), hyötyfunktio on muotoa
\[U(t,\ c) = v(t) + c,\]jossa \(v\) on kasvava funktio: \(v'(t)\gt0\), koska Angela haluaa vapaa-aikaa mieluummin enemmän kuin vähemmän. Tätä sanotaan kvasilineaariseksi funktioksi, koska hyöty on lineaarinen viljan kulutuksen \(c\) suhteen ja mahdollisesti epälineaarinen vapaa-ajan \(t\) funktio. Osoitamme nyt, että rajasubstituutiosuhde riippuu vain muuttujasta \(t\).
Angelan vapaa-ajan \(t\) ja viljan kulutuksen \(c\) rajasubstituutiosuhde on Leibniz-osion 3.2.1 määritelmän mukaisesti pisteen \((t,\ c)\) kautta kulkevan samahyötykäyrän kulmakertoimen itseisarvo. Sen voi laskea aiemman Leibniz-osion kaavasta
\[\text{MRS} = \frac{\partial U}{\partial t} \left/ \frac{\partial U}{\partial c} \right.\]Tässä tapauksessa \(\dfrac{\partial U}{\partial t} = v'(t)\) ja \(\dfrac{\partial U}{\partial c} = 1\), joten
\[\text{MRS} = v'(t).\]Samaan tulokseen voi päästä yleistä kaavaa käyttämättäkin. Jokainen samahyötykäyrä on muotoa
\[v(t) + c = \text{vakio}\]eli \(c= k - v(t)\), jossa \(k\) on vakio. Siksi
\[\frac{dc}{dt} = - v'(t) \lt0\]samahyötykäyrällä. Käyrä on laskeva, ja kulmakertoimen itseisarvo on \(v'(t)\). Rajasubstituutiosuhde on siis vain muuttujan \(t\) funktio, minkä halusimme todistaa.
Kuvion 1 samahyötykäyrillä on laskeva rajasubstituutiosuhde, joka loivenee oikealle päin mentäessä. Jotta näin käy, muuttujan \(v'(t)\) on laskettava muuttujan \(t\) kasvaessa. Siten \(v''(t)\lt0\): \(v\) on konkaavi funktio. Koska samahyötykäyrät ovat muotoa \('c = \text{vakio} - v(t)'\), jokaisen kahden käyrän välillä on vakioinen vertikaalinen etäisyys, kuten kuviossa 1. Kaavion käyrät kasautuvat muuttujan \(c\) suurilla arvoilla yhteen, koska käyrät ovat jyrkempiä.
Yhteenvetona: hyötyfunktio
\[U(t,\ c) = v(t) + c,\]jossa funktio \(v\) on kasvava ja konkaavi, sanotaan kvasilineaariseksi. Tämän muotoisen hyötyfunktion käyttö tarkoittaa, että teemme preferensseistä rajoittavan oletuksen, jolla on kuitenkin hyödyllinen seuraus. Koska hyöty on muotoa ‘\(c + \text{jotain}\)’, sen mittayksikkö on sama kuin kulutuksen. Angelan mielestä \(t\) tuntia vapaa-aikaa on samanarvoinen kuin \(v(t)\) vakkaa viljaa.
On hyödyllistä mitata hyötyä kulutusyksiköissä etenkin silloin, kun Angela voi myydä viljaa markkinoilla ja ostaa saamillaan tuloilla vaikkapa elintarvikkeita tai vaatteita. Tällaisissa tilanteissa muuttuja \(c\) tulkitaan usein rahatuloiksi. Kvasilineaaristen preferenssien oletus mahdollistaa hyödyn kasvun ja vähenemisen mittaamisen rahassa.
Esimerkki
Esimerkki kvasilineaarisesta hyötyfunktiosta on
\[U(t,\ c) = b t^\alpha + c,\]jossa \(b\) ja \(\alpha\) ovat positiivisia vakioita ja \(\alpha\lt1\). Heti näkee, että funktio on muotoa \(v(t) +c\) ja \(v(t)= b t^\alpha\). Jotta voimme osoittaa funktion edellä kuvatun kaltaiseksi kvasilineaariseksi hyötyfunktioksi, meidän on osoitettava, että funktio \(v\) on kasvava ja konkaavi. Se onnistuu helposti:
\[v'(t)= \alpha b t^{\alpha -1},\]joka on positiivinen, koska \(b\) ja \(\alpha\) ovat positiivisia ja
\[v''(t)= (\alpha -1)\alpha b t^{\alpha -2},\]joka on negatiivinen, koska \(b\gt0\) ja \(0\lt\alpha \lt1\).
Lisälukemista: Malcolm Pemberton ja Nicholas Rau. 2015. Mathematics for economists: An introductory textbook, 4. painos (luvut 17.1–17.3). Manchester: Manchester University Press.


