Leibniz 3.1.1 Keskituotos ja rajatuotos
Kuvioon 1 on piirretty Alexein tuotantofunktio, joka kuvaa hänen opiskeluun käyttämänsä ajan ja loppuarvosanan välistä yhteyttä. Totesimme, että jokaisessa käyrän pisteessä Alexein rajatuotos on tuotantofunktion kulmakerroin ja keskituotos pisteestä origoon kulkevan janan kulmakerroin. Seuraavaksi tarkastelemme rajatuotosta ja keskituotosta matemaattisesti.
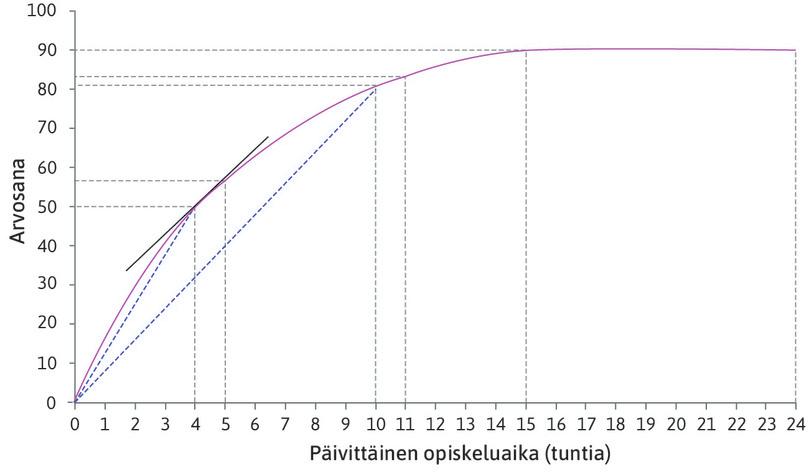
Kuvio 1 Miten Alexein opiskeluun käyttämä aika vaikuttaa hänen arvosanaansa?
Työtuntien ja arvosanan yhteyttä voi kuvata yleisesti yhtälöllä
\[y = f(h),\]jossa \(y\) on Alexein loppuarvosana (tuotanto) ja \(h\) päivittäisten työtuntien määrä (panos). \(f(h)\) on tuotantofunktio.
- keskituotos
- Kokonaistuotos jaettuna panoksella, esimerkiksi työntekijöiden määrällä tai käytettyjen työtuntien määrällä (tuotos työntekijää tai työtuntia kohti). Englanniksi average product.
Jos Alexei opiskelee \(h\) tuntia päivässä, voimme laskea hänen työnsä keskituotoksen jakamalla loppuarvosanan työtuntien määrällä:
\[\text{keskituotos} = \frac{y}{h} = \frac{f(h)}{h}\]Keskituotos on keskimääräinen pistesaalis päivittäistä opiskelutuntia kohti. Kaaviossa sitä vastaa origosta piirretyn janan kulmakerroin.
- rajatuotos
- Tuotoksen lisäys, joka saadaan lisäämällä jonkin panoksen määrää yhdellä yksiköllä, kun muiden panosten määrä pysyy ennallaan. Englanniksi marginal product.
Määrittelimme Alexein työn rajatuotoksen yhden tunnin lisäopiskelulla saavutettavaksi arvosanan parannukseksi. Tarkkaan ottaen rajatuotos mittaa sitä, miten nopeasti arvosana muuttuu työtuntimäärän kasvaessa. Se vastaa tuotantofunktion kulmakerrointa.
Oletetaan, että Alexei opiskelee \(h\) tuntia päivässä. Rajatuotos kertoo, miten paljon arvosana muuttuisi, jos opiskeluaika pitenisi \(\Delta h\) tunnilla. Jos arvosana paranee \(\Delta y\) pistettä, arvosanan muutos työtuntien muutosta kohti voidaan ilmaista osamääränä
\[\frac{\Delta y}{\Delta h} = \frac{f(h + \Delta h) - f(h)}{\Delta h}.\]Kun \(\Delta h\) lähenee nollaa, osamäärä lähenee tuotantofunktion derivaattaa. Matemaattisesti ilmaisten
\[\text{kun } \Delta h \to 0, \quad \frac{\Delta y}{\Delta h} \to \frac{dy}{dh},\]joka on tuotantofunktion kulmakerroin. Alexein rajatuotos \(h\) tunnin opiskelusta on siis tuotantofunktion derivaatta:
\[\text{rajatuotos} = \frac{dy}{dh}=f'(h)\]Olemme nyt määritelleet rajatuotoksen matemaattisesti. Rajasuureiden matemaattisia määritelmiä käytetään myös seuraavissa Leibniz-osioissa. Luvussa 3 selvitimme rajatuotoksen laskemalla, miten paljon tuotos kasvaa, kun panosta lisätään yhdellä yksiköllä. Se on hyvä likiarvo matemaattisesti määritellylle rajatuotokselle, mikäli yksiköt ovat pieniä. Esimerkiksi kuviossa 1 panoksen yksikkönä on tunti ja vaaka-akselin asteikko yltää 24 tuntiin. Yhden tunnin lisäyksestä seuraava tuotoksen kasvu vastaa funktion kulmakerrointa vain likimääräisesti. Jos vaaka-akselin yksikkönä olisi minuutti ja laskisimme tuotoksen kasvun yhden minuutin lisäystä kohti, tulos osuisi hyvin lähelle todellista kulmakerrointa.
Esimerkki
Kuvion 1 tuotantofunktiota vastaa ominaisuuksiltaan funktio
\[y = Ah^\alpha,\]jossa \(A\) ja \(\alpha\) ovat vakioita ja \(A \gt 0\), \(0 \lt \alpha \lt 1\). Nämä parametrit määräävät tuotantofunktion muodon ja sijainnin koordinaatistossa. Myöhempänä näytämme, miksi \(\alpha\) sijoittuu välttämättä arvojen 0 ja 1 välille. Esimerkkifunktiollamme on tuotantofunktion peruspiirteet: \(y=0\), kun \(h=0\); \(y\) on positiivinen, kun \(h\) on positiivinen.
Ehto \(\alpha \gt 0\) takaa, että tuotantofunktio on kasvava kaikilla \(h \geq 0\). Tämä on sinulle selvää, jos hallitset potenssilaskusäännöt. Todistamme funktion kasvavaksi myöhemmin osoittamalla, että rajatuotos on positiivinen. Ehdosta seuraa, että funktio poikkeaa hieman kuviosta 1, jossa funktion arvo on vakio, kun \(h \gt 15\) (kuvaaja pysyy tasaisena).
Esimerkkifunktiollemme työn keskituotos on
\[\text{keskituotos} = \frac{y}{h} = \frac{ Ah^\alpha }{h} = Ah^{\alpha-1}.\]Työn rajatuotos on tuotantofunktion derivaatta:
\[\text{rajatuotos} = \frac{dy}{dh} = A\alpha h^{\alpha -1}.\]Voimme nyt ilmaista rajatuotoksen toisin:
\[\text{rajatuotos} = \frac{\alpha}{h} \times Ah^\alpha = \frac{\alpha y}{h}.\]Tiedämme, että kun \(h\) on positiivinen, myös \(y\) on positiivinen. Rajatuotoksen yhtälöstä nähdään silloin heti, että ehdon \(\alpha \gt 0\) vallitessa työn rajatuotos on positiivinen: Alexein arvosana paranee, kun hän käyttää opiskeluun enemmän aikaa.
Entä ehto \(\alpha \lt 1\)? Koska työn keskituotos on \(\frac{y}{h}\) ja työn rajatuotos \(\frac{\alpha y}{h}\), \(\alpha\) on rajatuotoksen suhde keskituotokseen. Oletuksesta \(\alpha \lt 1\) seuraa silloin, että työn rajatuotos on pienempi kuin työn keskituotos. Se näkyy myös kuviosta 1, kun vertaa rajatuotosta eli käyrän kulmakerrointa keskituotokseen eli origosta lähtevän janan kulmakertoimeen pisteessä \(h=4\).
Tästä tuotantofunktion ominaisuudesta seuraa, että Alexein yhdellä lisätyötunnilla saavuttama pistemäärä jää aina pienemmäksi kuin hänen aiempien työtuntiensa keskimäärin tuottama pistemäärä, vaikka hän opiskelisi miten paljon tahansa.
Lisälukemista: Malcolm Pemberton ja Nicholas Rau. 2015. Mathematics for economists: An introductory textbook, 4. painos (luvut 6.1 ja 6.4). Manchester: Manchester University Press.


