Leibniz 7.8.1 Kysyntäjousto
Kysynnän hintajousto mittaa kysynnän muutosta hinnan muuttuessa: se kertoo kysynnän prosenttimääräisen muutoksen, kun hinta muuttuu yhden prosentin. Tässä Leibniz-osiossa määritämme jouston differentiaalilaskennan keinoin ja osoitamme, miten yrityksen hinnoittelupäätös riippuu kysynnän hintajoustosta.
Kysyntäfunktion voi kirjoittaa kahdella tavalla. Olemme aikaisemmin kuvanneet Ajattomien Autojen kysyntää käänteisellä kysyntäfunktiolla:
\[P = f(Q)\]Siinä \(f(Q)\) on hinta, jolla yritys saa myydyksi täsmälleen \(Q\) autoa. Jouston määrittämiseksi on kätevämpää kirjoittaa kysyntäfunktio suoraan:
\[Q = g(P)\]\(g(P)\) on Ajattomien Autojen kysyntä, jos hinta on \(P\). (Funktio \(g\) on funktion \(f\) käänteisfunktio; matemaattisesti voimme kirjoittaa \(g(P)=f^{-1}(P)\).)
Kysyntäfunktion derivaatta on \(dQ/dP=g'(P)\). Tämä on yksi tapa mitata, miten paljon kuluttajien kysyntä \(Q\) muuttuu, kun hinta muuttuu. Se ei ole kuitenkaan kovin hyödyllinen mittari, koska se riippuu siitä, missä yksiköissä muuttujia \(P\) ja \(Q\) mitataan. Jos hinnat ovat euroissa eivätkä dollareissa, saamme erilaisen vastauksen.
Sen sijaan määrittelemme kysynnän hintajouston tekstissä seuraavasti:
\[-\frac{\text{ kysynnän muutos (%)}}{\text{ hinnan muutos (%)}}\]Tämä on hyödyllisempi tapa kuvata kysynnän riippuvuutta hinnasta. Määritelmästä näkee, ettei se riipu mittausyksiköistä. Se liittyy kuitenkin läheisesti derivaattaan \(g'(P)\). Näemme sen, kun oletamme, että hinta muuttuu arvosta \(P\) arvoon \(P + \Delta P\), jolloin kysyntä muuttuu arvosta \(Q=g(P)\) arvoon \(Q + \Delta Q\). Hinnan prosentuaalinen muutos on \(100 \Delta P/P\) ja määrän prosentuaalinen muutos \(100 \Delta Q/Q\). Kun sijoitamme nämä joustolausekkeeseen, saamme:
\[\ -\frac{ \Delta Q}{Q} \left/ \frac{\Delta P}{P} \right. = -\frac{P}{Q} \, \frac{ \Delta Q}{ \Delta P}\]Kun \(\Delta P \to 0\), saamme kysynnän hintajouston matemaattisen määritelmän, josta käytämme merkintää \(\varepsilon\) niin kuin tekstissäkin:
\[\varepsilon = - \frac{P}{Q} \, \frac{ dQ}{dP}\]Koska \(Q=g(P)\), jouston voi kirjoittaa myös muotoon
\[\varepsilon = -\frac{Pg'(P)}{g(P)}.\]Huomaa, että jouston arvo on positiivinen, koska kysynnän lain mukaan kysyntäfunktion derivaatta on negatiivinen.
Differentiaalilaskennan keinoin määriteltynä \(\varepsilon\) on vain likimääräisesti sama kuin alkuperäinen määritelmämme, jonka mukaan jousto tarkoittaa kysynnän prosentuaalista muutosta, kun hinta nousee yhden prosentin. Mutta koska voimme kohtuullisesti olettaa, että yksi prosentti on pieni määrä, se on hyvä likiarvo, ja sellaiseksi se usein tulkitaan.
Tarkastele kysyntäfunktiota
\[Q=100 P^{-0,8}.\]Tässä
\[\varepsilon=-\frac{P}{Q}\,\frac{dQ}{dP} = -\frac{P}{100P^{-0,8}}\times -80P^{-1,8} = 0,8.\]Tässä nimenomaisessa tapauksessa kysyntäjousto on vakio: se on kaikissa kysyntäkäyrän pisteissä 0,8.
Yleensä jousto ei ole vakio. Se muuttuu, kun siirrytään kysyntäkäyrällä. Edellä oleva esimerkki havainnollistaa erikoistapausta. Jos kysyntäfunktio on muotoa \(Q = aP^{-c}\), jossa \(a\) ja \(c\) ovat positiivisia vakioita, kysyntäjousto on \(c\). Tämä on ainoa kysyntäfunktioiden luokka, jossa jousto on vakio.
Jouston ilmaiseminen suhteessa määrään
Kysyntäjouston voi ilmaista myös palaamalla kysyntäfunktion käänteisfunktioon \(P=f(Q)\). Käänteisfunktion säännön mukaan
\[\frac{dP}{dQ} = 1 \left/ \frac{dQ}{dP} \right. ,\]joten
\[\varepsilon = - \frac{P}{Q} \left/ \frac{dP}{dQ} \right. = - \frac{f(Q)}{Qf'(Q)}.\]Toinen esimerkki: oletetaan, että Ajattomilla Autoilla on käänteinen kysyntäfunktio
\[P= 8000 - 80 Q,\]kuten tekstin kuviossa 7.15. Edellä olevan lausekkeen perusteella kysyntäjousto on
\[\varepsilon=-\frac{8~000 -80 Q}{Q\times -80} = \frac{100}{Q} - 1.\]Voimme ilmaista jouston myös hinnan suhteen: \(Q=\dfrac{8~000-P}{80}\), joten
\[\varepsilon= -\frac{P}{Q}\, \frac{dQ}{dP} = -\frac{80P}{8~000 -P} \times -\frac{1}{80} = \frac{P}{8~000 -P}.\]Kumpikin jouston \(\varepsilon\) lauseke osoittaa, että jousto laskee, kun siirrytään kysyntäkäyrällä oikealle, jolloin \(Q\) kasvaa ja \(P\) laskee. Tämä pätee jokaiselle lineaariselle kysyntäfunktiolle, samoin tulokselle, että \(\varepsilon\) lähestyy arvoa \(0\), kun \(P\) lähestyy arvoa \(0\) ja \(\varepsilon\) arvoa \(\infty\) kun \(P\) lähestyy maksimiarvoaan, jossa \(Q=0\). Jos Ajattomat Autot myy vain kaksi autoa päivässä hintaan 7 840 euroa, kysyntäjousto on 49, mutta jos se myy 95 autoa päivässä hintaan 400 euroa, \(\varepsilon=0,053\) kolmen desimaalin tarkkuudella.
Jousto ja rajatulo
Näimme Leibniz-osiossa 7.6.1, että jos Ajattomien Autojen käänteinen kysyntäfunktio on \(f(Q)\), tulofunktio on
\[R(Q) = Qf(Q)\]ja rajatulo määritellään seuraavasti:
\[\text{MR} = R'(Q) = f(Q) + Qf'(Q).\]Kun kirjoitamme lausekkeen uudelleen ottamalla huomioon, että \(\varepsilon=-\dfrac{f(Q)}{Qf'(Q)}\) ja \(P=f(Q)\), näemme, että rajatulon ja kysyntäjouston välillä on yhteys:
\[\text{MR} = f(Q) - \frac{f(Q)}{\varepsilon} = P\left(1 - \frac{1}{\varepsilon}\right)\]Tämä tarkoittaa, että rajatulo on positiivinen, jos \(\varepsilon\gt1\), ja negatiivinen, jos \(\varepsilon\lt1\).
Kuten tekstissä todettiin, kysynnän sanotaan olevan joustava, jos \(\varepsilon\gt1\), ja joustamaton, jos \(\varepsilon\lt1\). Toinen esimerkki osoittaa, että kysyntä voi olla joustava joissain kysyntäkäyrän pisteissä ja joustamaton toisissa saman käyrän pisteissä. Olemme juuri osoittaneet, että rajatulo on positiivinen, jos ja vain jos yritys toimii kysyntäkäyrän sillä osalla, jolla kysyntä on joustavaa. Tämä pätee etenkin, jos yritys maksimoi voittonsa ja valitsee siksi tuotantonsa niin, että rajatulo ja rajakustannus ovat yhtä suuret, koska rajakustannus on positiivinen.
Suhteellinen voittomarginaali
Muistanet Leibniz-osiosta 7.6.1, että voiton maksimoinnin ensimmäisen kertaluvun ehto on \(\text{MR} = \text{MC}\), jossa \(\text{MC}\) on rajakustannus. Juuri johdetun rajatulon kaavan avulla voimme kirjoittaa ensimmäisen kertaluvun ehdon muodossa
\[(\varepsilon -1)P = \varepsilon \, \text{MC.}\]Järjestellään termit:
\[\frac{P - \text{MC}}{P} = \frac{1}{\varepsilon}\]Yhtälön vasen puoli on suhteellinen voittomarginaali eli voittomarginaalin \(P-\text{MC}\) osuus hinnasta. Yhtälö kertoo, että suhteellinen voittomarginaali on voiton maksimoivassa pisteessä sitä suurempi, mitä pienempi kysyntäjousto on. Jos kysyntäjousto on optimipisteessä \(5\), suhteellinen voittomarginaali on \(20\%\), kun taas kysyntäjousto \(1,25\) tarkoittaa, että suhteellinen voittomarginaali on \(80\%\), jolloin yritys asettaa hinnan viisinkertaiseksi rajakustannukseen verrattuna. Suhteellisen voittomarginaalin ja kysynnän hintajouston käänteinen suhde näkyy tekstin kuvioissa 7.16 ja 7.17, jotka on kopioitu tähän kuvioksi 1.
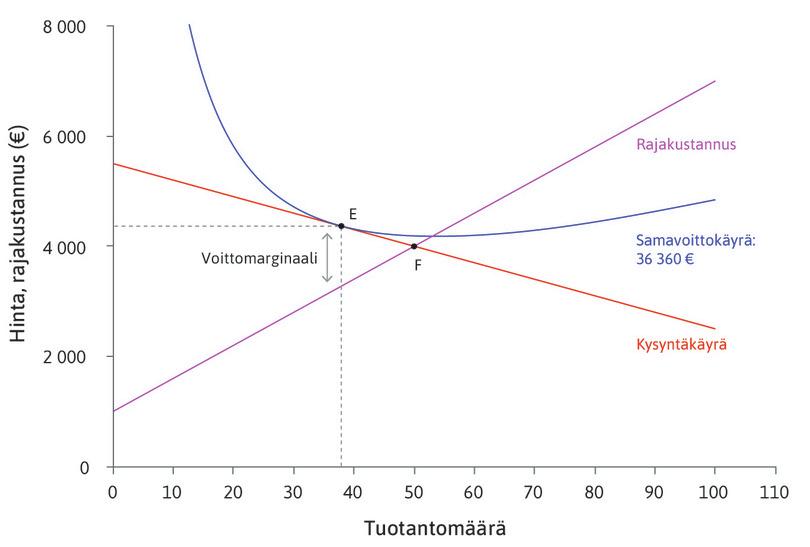
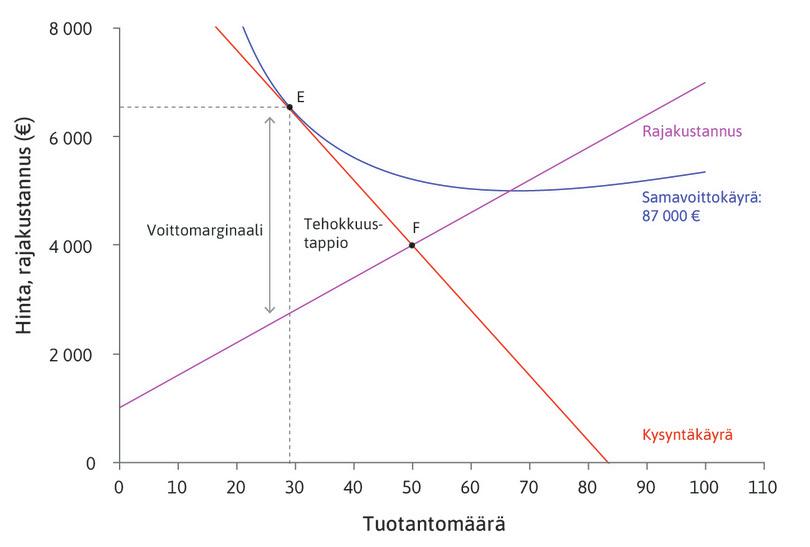
Kuvio 1 Voiton maksimointi, kun kysyntä on joustavaa (vasemmalla) ja joustamatonta (oikealla).
Jousto yleensä
Jousto on yleinen matemaattinen käsite, vaikka sitä käytetään tietääksemme vain taloustieteessä. Oletetaan, että on derivoituva funktio \(y=F(x)\), jossa muuttujilla \(x\) ja \(y\) on vain positiivisia arvoja. Muuttujan \(y\) jousto suhteessa muuttujaan \(x\) voidaan määritellä seuraavasti:
\[\frac{x}{y} \, \frac{dy}{dx} = \frac{xF'(x)}{F(x)}\]Tämä on raja-arvo suhdeluvulle
\[\frac{\text{ muuttujan } y \text{ muutos (%)}}{\text{ muuttujan } x \text{ muutos (%) }},\]kun nimittäjä lähestyy arvoa nolla. Vaihtoehto, jota käytimme kysynnän hintajoustossa, on määrittää jousto tämän raja-arvon itseisarvoksi.
Lisälukemista: Malcolm Pemberton ja Nicholas Rau. 2015. Mathematics for economists: An introductory textbook, 4. painos (luvut 6.4 ja 7.4). Manchester: Manchester University Press.


