Leibniz 8.4.2 Markkinoiden tasapainotila
Markkinat ovat kilpailullisessa tasapainossa, jos kaikki ostajat ja myyjät ovat hinnanottajia ja jos tarjonta on vallitsevalla markkinahinnalla yhtä suuri kuin kysyntä. Tässä Leibniz-osiossa näemme, miten tasapainohinta ja -määrä selvitetään matemaattisesti markkinoiden tarjonta- ja kysyntäkäyristä.
Kuvitellaan samanlaiset leipämarkkinat kuin luvussa 8: kaikki ostajat ja myyjät ovat hinnanottajia. Oletetaan, että markkinoiden kysyntäfunktio on \(Q = Q^D(P)\) ja markkinoiden tarjontafunktio \(Q = Q^S(P)\), samalla tavalla johdettuina kuin Leibniz-osiossa 8.4.1. Kysyntäkäyrä antaa kysynnän kokonaismäärän kullakin hinnalla ja tarjontakäyrä kokonaismäärän, jonka myyjät ovat valmiita tarjoamaan kullakin hinnalla. Leivän kysyntä ja tarjonta näkyy tekstin kuviossa 8.8 ja kopioituna oheiseen kuvioon 1 (muista, että hinta \(P\) piirretään yleensä pystyakselille ja määrä \(Q\) vaaka-akselille, joten kaaviossa näkyvät oikeasti käänteiset kysyntä- ja tarjontafunktiot).
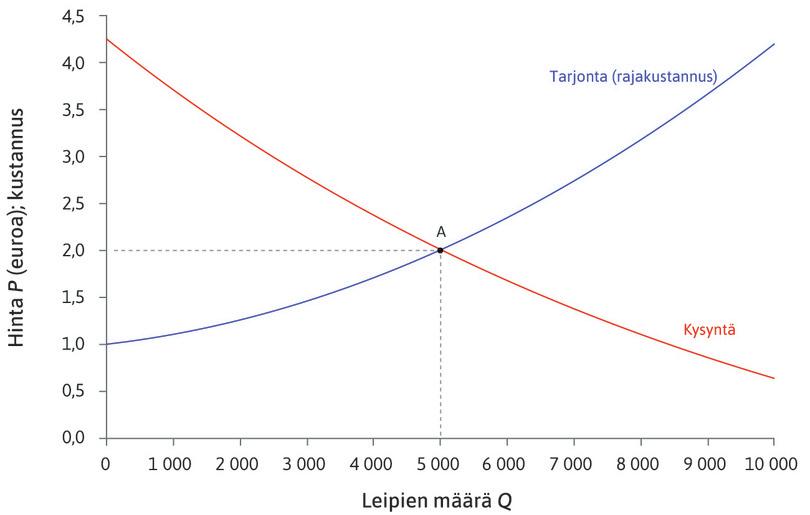
Kuvio 1 Leipämarkkinoiden tasapaino.
Tasapainohinnan ja -määrän selvittämiseksi on tarpeen ratkaista muuttujat \(P\) ja \(Q\) yhtälöparista.
Kun kysyntä- ja tarjontakäyrät ilmaistaan suorien kysyntä- ja tarjontafunktioiden \(Q^D\) ja \(Q^S\) suhteen, voimme etsiä aluksi tasapainohintaa eli hintaa, jolla kysyntä ja tarjonta ovat yhtä suuret. Tasapainohinta ratkaisee yhtälön
\[Q^D(P)=Q^S(P).\]Kuvion 1 kaltaisissa tapauksissa, joissa \(Q^S\) on kasvava ja \(Q^D\) vähenevä funktio, tasapainohintoja voi olla korkeintaan yksi. Kun tämän yhtälön ratkaisusta on saatu tasapainohinta, tasapainomäärä saadaan sijoittamalla tasapainohinta tarjonta- tai kysyntäyhtälöön. Kuviossa 1 tasapainohinta on 2 euroa ja vastaava määrä on 5 000 leipää.
Esimerkki
Olettakaamme, että markkinoiden kysyntä- ja tarjontafunktio ovat lineaarisia:
\[Q^D(P)=a-bP, \quad Q^S(P)=c+dP,\]jossa \(a,\ b,\ c,\ d\) ovat vakioita. Oletamme, että \(b \gt 0\) ja \(d \gt 0\). Tämä on siis tyypillisin tapaus, jolloin kysyntä on laskeva ja tarjonta nouseva. Jotta hyödykkeelle on kysyntää, kun hinta on riittävän alhainen, ehdon \(a \gt 0\) pitää täyttyä. Oletamme myös, että \(a \gt c\). (Jos \(a \leq c\), tarjonta ylittää kysynnän kaikilla positiivisilla hinnoilla. Kun totesimme edellä, että tasapainohintoja on korkeintaan yksi, otimme huomioon tapauksen, jossa tasapainohintaa ei ole.)
Tasapainohinta \(P^*\) toteuttaa yhtälön
\[a-bP=c+dP.\]Ratkaisemme yhtälön
\[P^*=\frac{a-c}{b+d}\]ja saamme tasapainotilan kysynnän ja tarjonnan \(Q^*\) seuraavasta:
\[Q^*= a-bP^* = \frac{ad+bc}{b+d}\]\(Q^*\) on positiivinen jos ja vain jos \(ad+bc\gt0\). Ellei tämä ehto toteudu, sellaista markkinatasapainoa ei ole, jossa hyödykettä menee kaupaksi.
Lisälukemista: Malcolm Pemberton ja Nicholas Rau. 2015. Mathematics for economists: An introductory textbook, 4. painos (luku 1.2). Manchester: Manchester University Press.


