Leibniz 8.6.1 Kysynnän ja tarjonnan siirtymät
Kilpailullinen tasapainohinta ja määrä ovat pisteessä, jossa kysyntä- ja tarjontakäyrät leikkaavat. Jos toinen käyrä siirtyy sokin seurauksena, sekä tasapainohinta että määrä muuttuvat. Tässä Leibniz-osiossa osoitamme, miten tarjonta- tai kysyntäsokin vaikutuksia voi mallintaa matemaattisesti.
Saamme markkinoiden kilpailullisen tasapainohinnan ja -määrän ratkaisemalla hinnan P ja määrän Q simultaaniyhtälöparista, jonka muodostavat kysyntäkäyrä \(Q=Q^D(P)\) ja tarjontakäyrä \(Q=Q^S(P)\). Kilpailullisella tasapainohinnalla kysyntä ja tarjonta ovat yhtä suuret:
\[Q^D(P)=Q^S(P)\]Kuten Leibniz-osiossa 8.4.2 näimme, jos tiedämme kysyntä- ja tarjontafunktiot, voimme ratkaista tästä yhtälöstä tasapainohinnan ja selvittää sen perusteella tasapainomäärän. Mutta mitä tapahtuu, jos toinen funktioista muuttuu?
Tarkastellaan Leibniz-osion 8.4.2 tapausta, jossa markkinoiden tarjonta- ja kysyntäfunktiot ovat lineaarisia:
\[Q^D(P)=a-bP, \quad Q^S(P)=c+dP,\]jossa \(a, b, c, d\) ovat vakioita. Oletetaan jälleen, että a, b ja d ovat positiivisia, jolloin kysyntäkäyrä on laskeva ja tarjontakäyrä nouseva. Sen vuoksi tasapainohintoja on enintään yksi. Osoitimme aikaisemmin, että jos \(a \gt c\) ja \(ac + bd \gt 0\), on olemassa positiivinen tasapainohinta \(P^*\) ja positiivinen tasapainomäärä \(Q^*\):
\[P^*=\frac{a-c}{b+d}, \quad Q^*= a-bP^* = \frac{ad+bc}{b+d}\]Oletetaan, että markkinoilla tapahtuu positiivinen kysyntäsokki ja kysyntä kasvaa jokaisella hinnan arvolla. Voimme mallintaa kysyntäsokkia parametrin a muutoksella \(\Delta a\). Uusi kysyntäkäyrä on \(Q=a+\Delta a-bP\), jossa \(\Delta a \gt 0\) vastaa positiivista sokkia; \(\Delta a \lt 0\) vastaisi negatiivista sokkia, jolloin kysyntä laskisi hinnan jokaisella arvolla.
Uuden tasapainohinnan \(P^*\) ja -määrän \(Q^*\) voi ratkaista uuden kysyntäkäyrän yhtälöstä samalla tavalla kuin ennen. Helpompi ja nopeampi tapa on käyttää hinnan \(P^*\) ja määrän \(Q^*\) lausekkeita ja laskea, miten ne muuttuvat, kun a muuttuu:
\[\Delta P^*=\frac{\Delta a}{b+d}, \quad \Delta Q^*= \frac{d\Delta a}{b+d}\]Voit tarkistaa tulokset halutessasi kirjoittamalla auki muutaman välivaiheen. Esimerkiksi hinnan \(P^*\) muutos saadaan seuraavasti:
\[\Delta P^*=\frac{a+\Delta a-c}{b+d}-\frac{a-c}{b+d}=\frac{\Delta a}{b+d}\]Näistä lausekkeita \(\Delta P^*\) ja \(\Delta Q^*\) näkee heti, että kysynnän kasvu (\(\Delta a \gt 0\)) nostaa sekä tasapainohintaa että -määrää. Huomaa, että jos kysyntä millä tahansa hinnalla nousee yhden yksikön (\(\Delta a = 1\)), tasapainotilan kysytyn ja tarjotun määrän muutos on \(d/(b+d)\), joka on positiivinen mutta pienempi kuin \(1\). Niinpä kysynnän kasvu tarkoittaa, että kuluttajat ostavat enemmän, mutta samalla hintakin nousee ja kuluttajat ostavat vähemmän kuin ilman hinnanmuutosta.
Tässä analysoitu kysyntäsokki on samanlainen kuin kuvion 8.11 esimerkissä kirjojen kysynnän kasvusta. Kuvio on kopioitu tähän kuvioksi 1. Kirjojen tarjonta- ja kysyntäfunktiot ovat lineaarisia. Kaavio osoittaa, että jos kirjojen määrä kasvaa kullakin hinnalla, kysyntäkäyrä siirtyy oikealle ja sekä tasapainohinta että -määrä nousevat. Ainoa ero on siinä, että parametrin a muutos \(\Delta a\) aiheuttaa kysyntäkäyrän siirtymisen samassa suunnassa, kun taas kuviossa 1 myös kulmakerroin muuttuu.
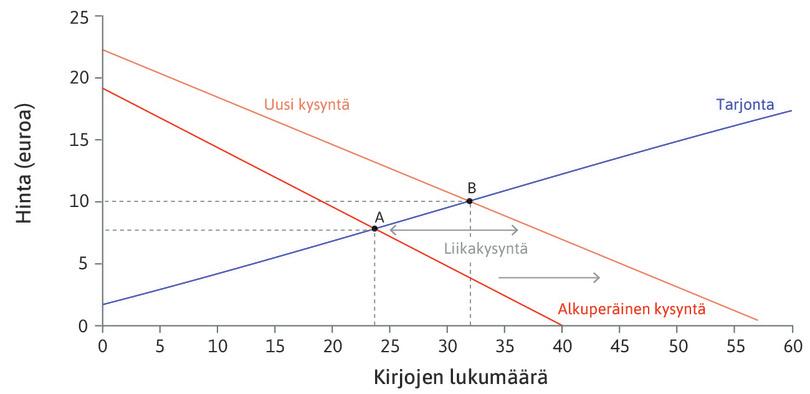
Kuvio 1 Kirjojen kysynnän kasvu.
Tarkastelimme tekstissä myös positiivista tarjontasokkia. Teknologian parannuksen ansiosta leipomot pystyivät tuottamaan enemmän alhaisemmalla hinnalla. Kuvasimme tätä kuviossa 8.12, joka on kopioitu tähän kuvioksi 2. (Kysyntä- ja tarjontakäyrät eivät ole tässä kaaviossa lineaarisia, mutta periaate on sama.) Kun leipomisen rajakustannus laskee, leipomoiden tarjontakäyrä siirtyy alaspäin ja markkinoiden uusi tasapaino on pisteessä B.
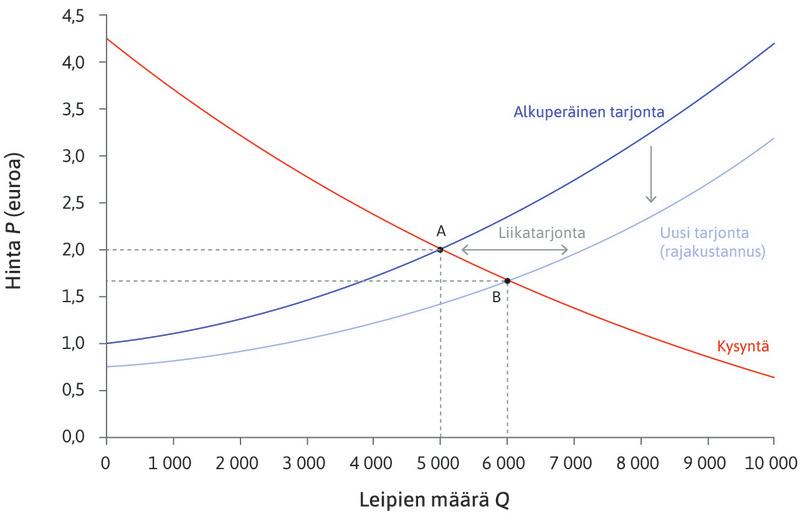
Kuvio 2 Leivän tarjonnan kasvu: rajakustannus laskee.
Tällainen tarjontasokki tarkoittaa, että leipomot haluavat tarjota jokaisella hinnalla enemmän leipää. Sitä voi kuvata lineaarisessa esimerkissämme parametrin c muutoksella \(\Delta c \gt 0\). (\(\Delta c \lt 0\) tarkoittaisi taas, että yritykset tarjoaisivat jokaisella hinnalla vähemmän leipää.) Muutoksen vaikutus tasapainohintaan ja -määrään on
\[\Delta P^*= - \frac{\Delta c}{b+d}, \quad \Delta Q^*= \frac{b\Delta c}{b+d}.\](Voit jälleen tarkistaa laskutoimituksen kirjoittamalla välivaiheet auki itse.)
Tässä tapauksessa \(\Delta c \gt 0\), joten sokki nostaa määrää ja laskee hintaa, niin kuin kuvio 2 kertoo.
Epälineaarinen kysyntä ja tarjonta
Jos kysyntä- ja tarjontakäyrät eivät ole lineaarisia, tasapainohintaan ja -määrään voi olla vaikeaa löytää tarkkaa ratkaisua. Silloinkin on mahdollista mallintaa jompaakumpaa käyrää siirtävän sokin vaikutusta ja päätellä, miten se vaikuttaa tasapainoon. Luvun 8 leipämarkkinaesimerkissä teimme tämän graafisesti. Tässä teemme saman matemaattisesti.
Kirjoitamme leivän kysyntäkäyrän muotoon \(Q=Q^D(P,\ a)\). Kysyntä laskee hinnan P mukana, mutta kysyntä riippuu myös parametrista a, joka kuvaa kuluttajan makua. Parametrin suuri arvo kuvaa tilannetta, jossa kuluttajat ovat persoja leivälle ja ostavat sitä paljon millä tahansa hinnalla. Kun a on pieni, leipää kysytään vähemmän joka hinnalla. Kysynnän riippuvuutta hinnasta P ja parametrista a voi kuvata osittaisderivaattojen avulla:
\[\frac{\partial Q^D}{\partial P} \lt 0; \quad \frac{\partial Q^D}{\partial a} \gt 0\]Positiivista kysyntäsokkia vastaa parametrin a kasvu. Se lisää kysyntää jokaisella hinnalla. Kun kysyntäkäyrä piirretään \((Q,\ P)\)-avaruuteen, pidämme parametrin a arvon kiinteänä. Parametrin a kasvu siirtää kysyntäkäyrää oikealle. Lasku taas edustaa negatiivista kysyntäsokkia ja siirtää käyrää vasemmalle.
Kirjoitetaan leivän tarjontakäyrä vastaavasti muodossa \(Q=Q^S(P,\ c),\) jossa parametri c mallintaa tarjontasokkeja. Voimme ajatella, että c edustaa teknologiaa. Parametrin c kasvu vastaa teknologian parannusta, joka alentaa leivän tuottamisen rajakustannusta ja tarkoittaa, että leipomot tarjoavat jokaisella hinnalla enemmän leipää. Osittaisderivaatoilla ilmaistuna:
\[\frac{\partial Q^S}{\partial P} \gt 0; \quad \frac{\partial Q^S}{\partial c} \gt 0\]Teknologian parannusta vastaa parametrin c kasvu, joka siirtää tarjontakäyrää oikealle. Tämä näkyy kuviossa 2.
Millä tahansa parametrien a ja c arvoilla kysyntäkäyrä on laskeva ja tarjontakäyrä nouseva avaruudessa \((Q,\ P)\). Tasapainohintoja \(P^*\) on siis enintään yksi, samoin sitä vastaavia tasapainomääriä \(Q^*.\) Mutta jos a ja c muuttuvat, myös \(P^*\) ja \(Q^*\) muuttuvat. Siten \(P^*\) ja \(Q^*\) riippuvat parametreista a ja c. Voimme ilmaista ne hinnan ja määrän funktioina:
\[P^* = F(a,\ c), \quad Q^* = G(a,\ c)\]Haluamme tietää, miten \(P^*\) ja \(Q^*\) muuttuvat, kun a ja c muuttuvat. Haluamme toisin sanoen tietää muuttujien a ja c suhteen laskettujen hinnan \(P^*\) ja määrän \(Q^*\) osittaisderivaattojen etumerkit. Selvitämme ne käyttämällä implisiittistä derivointia. Aloitamme osittaisderivaatoilla muuttujan a suhteen. Ne kertovat, miten kysyntäsokki vaikuttaa tasapainoon.
Tasapainohinta \(P^*\) toteuttaa markkinoiden tasapainoyhtälön
\[Q^D(P^*,\ a)=Q^S(P^*,\ c).\]Derivoimme sitten yhtälön molemmat puolet muuttujan a suhteen muistaen, että \(P^*\) on muuttujan a funktio (eli \(P^* = F(a,\ c)\)). Saamme:
\[\frac{\partial Q^D}{\partial P} \frac{\partial P^*}{\partial a}+ \frac{\partial Q^D}{\partial a} =\frac{\partial Q^S}{\partial P} \frac{\partial P^*}{\partial a}\]Järjestellään termit niin, että voimme ilmaista osittaisderivaatan \(\partial P^*/\partial a\) muiden osittaisderivaattojen suhteen:
\[\frac{\partial P^*}{\partial a} =\frac{\frac{\partial Q^D}{\partial a}} {\frac{\partial Q^S}{\partial P}-\frac {\partial Q^D}{\partial P} }.\]Murtoluvun nimittäjä on positiivinen, koska \(\partial Q^S/\partial P \gt 0\) and \(\partial Q^D/\partial P \lt 0\). Kysyntäfunktiosta tiedämme, että myös osoittaja on positiivinen. Siten \(\partial P^*/\partial a \gt 0\). Positiivinen kysyntäsokki (parametrin a kasvu) johtaa siis tasapainohinnan nousuun.
Saamme osittaisderivaatan \(\partial Q^*/\partial a\) määrän \(Q^*\) yhtälöstä
\[Q^*=Q^S(P^*,\ c)\]muistaen taas, että \(P^*\) on muuttujan a funktio. Derivoidaan muuttujan a suhteen:
\[\frac{\partial Q^*}{\partial a} =\frac{\partial Q^S}{\partial P^*} \frac{\partial P^*}{\partial a}\]Koska \(\partial Q^S/\partial P^*\gt0\) ja olemme juuri osoittaneet, että \(\partial P^*/\partial a\gt0\), voimme päätellä, että myös \(\partial Q^*/\partial a\gt0\). Positiivinen kysyntäsokki (parametrin a kasvu) johtaa sekä tasapainohinnan että tasapainomäärän kasvuun, kun taas negatiivisella kysyntäsokilla on päinvastainen vaikutus.
Tarjontasokin vaikutuksen saamme selville osittaisderivoimalla hinnan \(P^*\) ja määrän \(Q^*\) muuttujan c suhteen. Se käy samalla tavalla. Derivoimme ensin markkinoiden tasapainoyhtälön parametrin c suhteen, jotta saamme selville osittaisderivaatan \(\partial P^*/\partial c\) etumerkin. Sen jälkeen selvitämme osittaisderivaatan \(\partial P^*/\partial c\) etumerkin tarjontakäyrän tai kysyntäkäyrän yhtälöstä (jälkimmäinen vaihtoehto on tässä tapauksessa helpompi). Jos teet tämän huolellisesti, huomaat, että \(\partial P^*/\partial c\lt0\) ja \(\partial Q^*/\partial c\gt0\), joten positiivinen tarjontasokki lisää määrää ja laskee hintaa.
Kysyntä- ja tarjontasokit vaikuttavat siis tasapainohintaan ja -määrään samalla tavalla kuin luvun 8 kaavioissa riippumatta kysyntä- ja tarjontafunktioiden täsmällisestä muodosta, kunhan niillä on tavanomaiset ominaisuudet eli kysyntäkäyrä on laskeva ja tarjontakäyrä nouseva.
Lisälukemista: Malcolm Pemberton ja Nicholas Rau. 2015. Mathematics for economists: An introductory textbook, 4. painos (luku 15.2 ja luvun 15.3 kaksi ensimmäistä kappaletta). Manchester: Manchester University Press.


