Leibniz 6.7.1 Voitto, palkat ja työpanos
Marian ja työnantajan vuorovaikutuksessa työnantaja valitsee palkan ja Maria vastaa valitsemalla työpanoksensa tason. Tässä Leibniz-osiossa tarkastelemme matemaattisesti työnantajan palkanasetantapäätöstä.
Miten suureksi Marian työnantajan kannattaa palkka asettaa? Osoitamme ensin, että maksimoidakseen voittonsa työnantajan on valittava palkka siten, että työpanoksen yksikkökustannus minimoituu, kun Marian vaste huomioidaan.
Jos Maria työskentelee työnantajalleen \(H\) tuntia viikossa ja hänen työpanoksensa on \(e\), hän tekee tuottavaa työtä \(N\) tuntia viikossa, missä \(N=eH\). Olkoon työnantajan tuotantofunktio \(f(N)\). Oletetaan, että yritys myy tuotoksensa hintaan \(p\). Merkitsemme työnantajan voittoja kreikan kirjaimella iso pii, \(\Pi\). Voitot voi kirjoittaa yhtälöksi
\[\Pi=pf(eH)-wH.\]Työnantaja voi päättää vapaasti palkan ja Marian työajan. Maria päättää omasta työpanoksestaan. Työnantajan tavoitteena on valita \(w\) ja \(H\), joilla \(\Pi\) maksimoituu, kun hän tietää, että Marian vaste palkkapäätökseen on aina
\[e = E(w).\]Ongelman muotoilusta ei heti käy ilmi, että työnantajan tulisi valita työpanoksen kustannuksen \(w/e\) minimoiva palkkataso, vaikka alaluvussa 6.7 niin totesimmekin. Asia kirkastuu matemaattisesti, kun ilmaisemme voiton muuttujien \(w\) ja \(N\) funktiona; \(N\) on tuotannossa käytetty panos. Sijoitamme voittofunktioon lausekkeen \(H=N/e\):
\[\Pi=pf(N)-\frac{w}{e}N \text{, jossa } e=E(w).\]Voitto riippuu siis työn yksikkömäärästä \(N\) ja työn (työpanoksen) yksikkökustannuksesta \(w/e\). Tämän yhtälömuodon perusteella on selvää, että työnantajan tulisi valita palkkataso, jolla kustannus \(w/e\) on mahdollisimman pieni.
Palkan asettaminen
Osoitimme äsken, että työnantajan on valittava palkka siten, että työpanoksen yksikkökustannus \(w/e\) minimoituu, kun Maria valitsee vasteen \(e=E(w)\). Osamäärän derivointisääntöä soveltamalla saadaan
\[\frac{d}{dw} \left(\frac{w}{E(w)}\right) = \frac{E(w)-wE'(w)}{E(w)^2}.\]Merkitsemällä lausekkeen nollaksi saamme ensimmäisen kertaluvun optimointiehdon työnantajan kustannusten minimoimiselle. Kustannukset minimoiva palkka \(w^*\) toteuttaa yhtälön
\[E'(w^*)= E(w^*)/w^*.\]Toista derivaatan merkintätapaa käyttämällä
\[\frac{de}{dw} = \frac{e}{w}.\]Palkkaehtoa havainnollistaa kuvio 1, joka on sama kuin luvun 6 kuvio 6.6. Kuvion suorat ovat työpanoksen samakustannuskäyriä. Niiden kulmakerroin on \(e/w\). Piste A toteuttaa äsken johtamamme yhtälön: samakustannuskäyrän kulmakerroin \(e/w\) on yhtä suuri kuin työntekijän parhaan vasteen käyrän kulmakerroin \(de/dw\). Kuvion parhaan vasteen käyrällä \(w^*=12\), ja sitä vastaava työpanoksen taso on \(E(w^*)\) = 0,5.
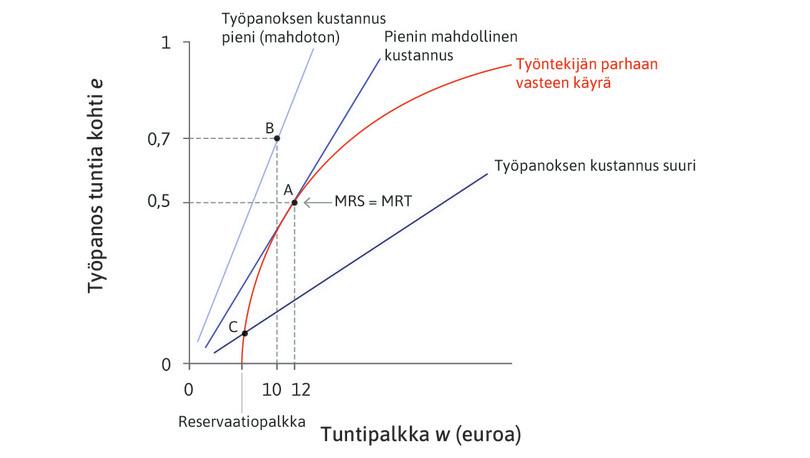
Kuvio 1 Työpanoksen kustannuksen minimointi.
Työpanoksen yksikkökustannus on matalampi jyrkemmillä samakustannuskäyrillä: \(e/w\) on suurempi ja \(w/e\) pienempi. Parhaan vasteen käyrällä kustannus minimoituu silloin pisteessä A. Voimme tarkistaa matemaattisesti, että ensimmäisen kertaluvun optimiehdon toteuttava palkka \(w^*\) on funktion \(w/E(w)\) minimi. Sitä varten on todistettava, että funktion toinen derivaatta on positiivinen, kun \(w=w^*\). Jos teet todistustehtävän, voit huomata kiinnostavan seikan: parhaan vasteen käyrän konkaaviudesta eli matemaattisesta ehdosta \(E’’(w)\lt0\) seuraa, että kustannukset todella minimoituvat palkan arvolla \(w^*\).
Työajan päättäminen
Kun voiton maksimoiva ja kustannukset minimoiva palkka \(w^*\) tunnetaan, työnantaja voi päätellä voiton maksimointiin tarvittavan työpanosyksiköiden määrän \(N\). Jos palkka on \(w^*\), voitto on
\[\Pi=pf(N)-\frac{w^*}{E(w^*)}N.\]Derivoimalla voittofunktion muuttujan N suhteen ja merkitsemällä derivaatan nollaksi saamme voiton maksimoivaa panosta \(N^*\) kuvaavan yhtälön:
\[pf'(N^*) = \frac{w^*}{E(w^*)}\]Yhtälöllä on taloustieteellinen tulkinta. \(f’(N)\) on yhden lisätyöpanosyksikön rajatuotos, joten \(pf’(N)\) on työnantajan yhdestä työpanosyksiköstä saama rajatulo. Työnantaja voi maksimoida voittonsa valitsemalla työpanosyksiköiden määrän \(N\) siten, että rajatulo on yhtä suuri kuin lisäyksikön rajakustannus \(w^*/E(w^*)\).
Työpanosyksiköiden optimaalinen määrä \(N^*\) on nyt selvillä, ja lisäksi tiedämme, että Maria valitsee työpanoksensa tasoksi \(E(w^*)\). Työnantaja voi nyt laskea tarvittavan työajan yhtälöstä \(H=N/e\).
Esimerkki
Olkoon Marian reservaatiopalkka positiivinen vakio \(w_r\) ja parhaan vasteen funktio
\[E(w) = k(w-w_r)^\alpha \quad (w\gt w_r),\]jossa \(k\) ja \(\alpha\) ovat myös positiivisia vakioita ja \(\alpha \lt1\). Voiton maksimoiva palkka \(E'(w^*)= E(w^*)/w^*\) toteuttaa ensimmäisen kertaluvun optimiehdon
\[\alpha k(w^* -w_r)^{\alpha-1} = k(w^*-w_r)^\alpha /w^*.\]Jakamalla oikeanpuoleisella termillä saamme yhtälön \(\alpha w^*/(w^* -w_r) =1\), jolloin
\[w^* = \frac{w_r}{1 - \alpha}.\]Huomaa, että \(w^*\) riippuu reservaatiopalkasta \(w_r\) ja parhaan vasteen funktion eksponentista \(\alpha\) muttei funktion kertoimesta \(k\). Kuvio 1 esittää esimerkkitapausta, jossa \(w_r =6\), \(\alpha=0,5\) ja \(k = 0,5/\sqrt{6}\).
Työnantaja asettaa palkan \(w^* = w_r/(1 - \alpha)\), ja Maria vastaa valitsemalla työpanoksen
\[E(w^*) = k \left(\frac{\alpha w_r}{1 - \alpha}\right)^\alpha.\]Lisälukemista: Malcolm Pemberton ja Nicholas Rau. 2015. Mathematics for economists: An introductory textbook, 4. painos (luvut 7.1 ja 8.1). Manchester: Manchester University Press.


