Leibniz 3.1.2 Laskeva rajatuottavuus
Alexein tuotantofunktion ominaisuuksiin kuuluu, että rajatuottavuus on laskeva. Funktion kuvaaja tasaantuu päivittäisten työtuntien määrän kasvaessa. Millaiset matemaattiset ominaisuudet vastaavat laskevaa rajatuottavuutta?
Jos tuotantofunktio on \(y=f(h)\), työn rajatuotos on \(\frac{dy}{dh}=f’(h)\). Rajatuotos pienenee muuttujan \(h\) kasvaessa, jos
\[\frac{d}{dh}\left( \frac{dy}{dh} \right) = \frac{d^{2}y}{dh^{2}} < 0\]tai toista merkintätapaa käyttäen
\[f’’(h) \lt 0.\]Tuotantofunktion toisen derivaatan tulee siis olla negatiivinen.
Esimerkki
Tarkastellaan jälleen tuotantofunktiota
\[y = Ah^\alpha,\]jossa \(A\) ja \(\alpha\) ovat vakioita ja \(A \gt 0\), \(0 \lt \alpha \lt 1\). Osoitimme Leibniz-osiossa 3.1.1, että tällaisen tuotantofunktion rajatuotos on seuraava:
\[\text{rajatuotos} = \frac{dy}{dh} = \alpha Ah^{\alpha -1},\]joka on positiivinen tuntimäärän \(h\) positiivisilla arvoilla. Haluamme nyt osoittaa, että tuntimäärän \(h\) kasvaessa rajatuotos pienenee.
Eräs tapa on tarkastella rajatuotoksen lauseketta
\[\alpha Ah^{\alpha -1}.\]Muuttuja \(h\) saa eksponentin \(\alpha -1\), joka on negatiivinen, koska \(\alpha \lt 1\). Negatiivisten eksponenttien ominaisuuksiin kuuluu, että muuttujan \(h\) kasvaessa \(h^{\alpha -1}\) pienenee. Koska vakiot \(A\) ja \(\alpha\) ovat positiivisia, myös työn rajatuotos \(\alpha Ah^{\alpha -1}\) pienenee.
Toinen tapa on derivoida rajatuotos:
\[\frac{d^2 y}{dh^2} = (\alpha -1)\alpha Ah^{\alpha -2}= \alpha(\alpha -1)\frac{Ah^\alpha}{h^2} =\alpha(\alpha -1)\frac{y}{h^2}\]Tiedämme, että positiivisilla tuntimäärän \(h\) arvoilla myös tuotos \(y\) on positiivinen. Koska \(0 \lt \alpha \lt 1\), niin \(\alpha(\alpha -1) \lt 0\), josta seuraa
\[\frac{d^2 y}{dh^2} =\alpha(\alpha -1)\frac{y}{h^2} \lt 0.\]Olemme osoittaneet, että tuotantofunktion toinen derivaatta on negatiivinen, jolloin rajatuotos pienenee muuttujan \(h\) kasvaessa. Toisin sanoen työn rajatuotos on laskeva.
Leibniz-osiossa 3.1.1 osoitimme, että kun \(\alpha \lt 1\), rajatuotos on pienempi kuin keskituotos. Tämä tuotantofunktion ominaisuus liittyy kiinteästi laskevaan rajatuottavuuteen: jos tuotantofunktion rajatuotos on laskeva kaikilla panoksen arvoilla, rajatuotos on pienempi kuin keskituotos.
Kuvioon 2 on piirretty tuotantofunktio \(y = Ah^\alpha\), jossa \(\alpha =0,4\) ja \(A=30\), sekä työn rajatuotoksen kuvaaja. Jokaiselle muuttujan \(h\) arvolle voi ylemmästä kaaviosta lukea funktion \(y\) arvon ja alemmasta kaaviosta tuotantofunktion kulmakertoimen \(dy/dh\). Kuviosta näemme, että työn rajatuotos laskee muuttujan \(h\) kasvaessa.
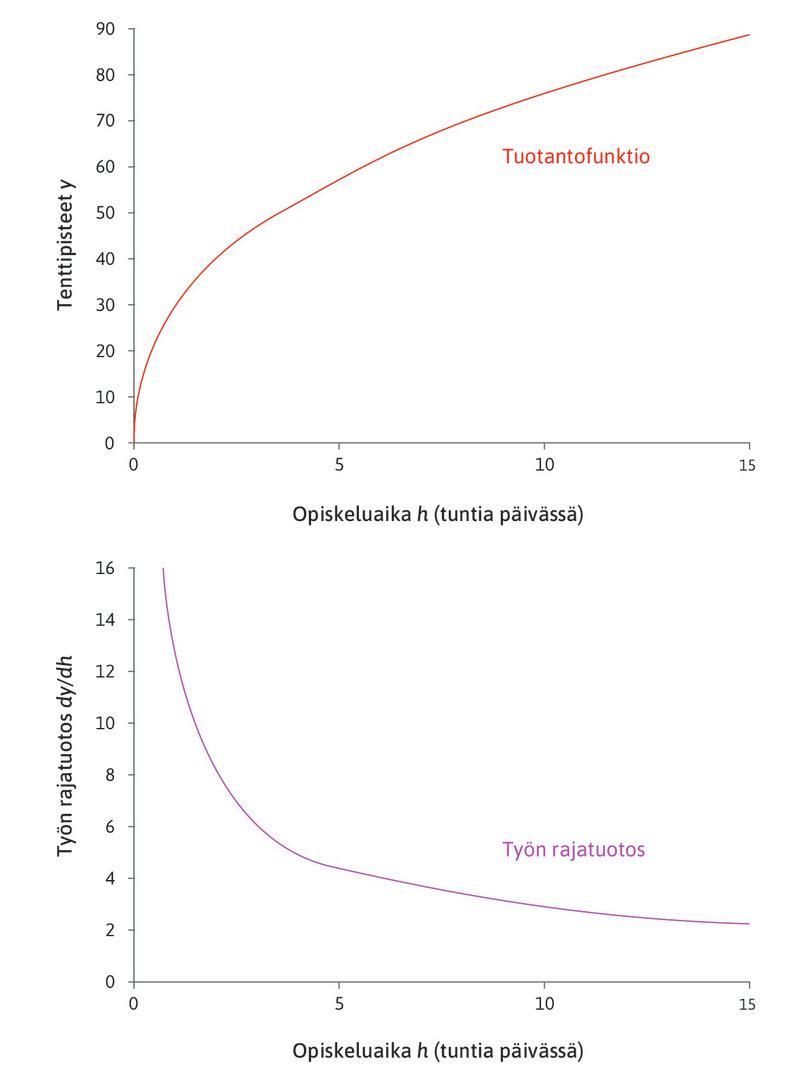
Kuvio 2 Tuotantofunktio y = 30h0,4 ja funktion rajatuotos.
Lisälukemista: Pemberton ja Rau (2016), luvut 6.4 ja 8.4.


