Leibniz 3.6.1 Teknologisen muutoksen mallintaminen
Viljelijä Angelan näkökulmasta teknologinen muutos tarkoittaa, että hän saa samalla työllä entistä suuremman sadon. Teknologisen muutoksen voi mallintaa matemaattisesti tuotantofunktion parametrien muutokseksi.
Kuviossa 1 on luvun 3 kuviosta 3.12 tuttu teknologisen kehityksen kuvaaja. Kuviossa Angelan tuotantofunktio siirtyy ylöspäin, koska hän pystyy tuottamaan entistä enemmän viljaa työtuntia kohti.
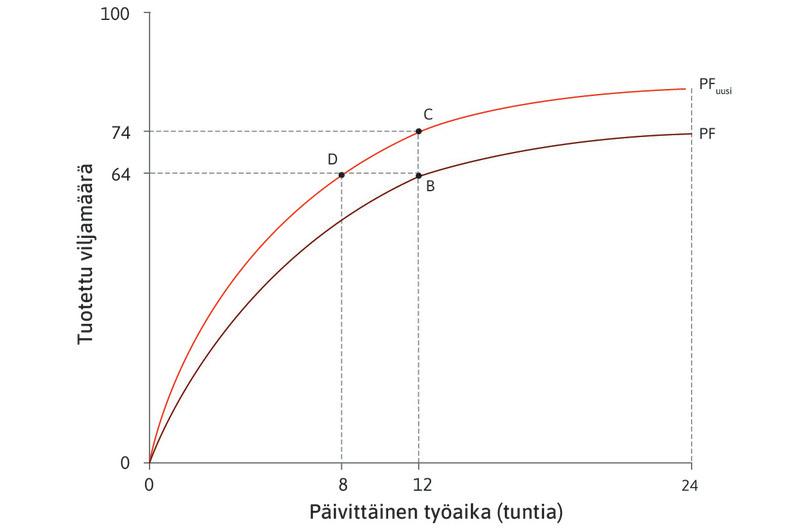
Kuvio 1 Angelan tuotantofunktio siirtyy ylöspäin.
Tähän saakka olemme käyttäneet tuotantofunktiota
\[y = Ah^\alpha\](katso esimerkiksi Leibniz-osio 3.1.2).
Muuttuja \(h\) kuvaa Angelan päivittäistä työaikaa, muuttuja \(y\) päivittäistä tuotosta. Funktion parametrit \(A\) ja \(\alpha\) määräävät tuotantofunktion muodon ja sijainnin koordinaatistossa. Olemme olettaneet, että \(A \gt 0\) ja \(0 \lt \alpha \lt 1\). Ensimmäinen oletus tarkoittaa yksinkertaisesti, että työ tuottaa viljaa eikä tuhoa sitä. Toinen oletus tarkoittaa, että työn rajatuotos on laskeva ja tuotantofunktio siis konkaavi.
Teknologinen kehitys merkitsee, että entisellä panosmäärällä voi tuottaa enemmän. Tuotantofunktiossamme sama työtuntimäärä johtaa nyt suurempaan viljamäärään. Teknologista kehitystä voi kuvata tuotantofunktiossa matemaattisesti kahdella tavalla.
Jos kerroin \(A\) kasvaa, myös tuotanto kasvaa kaikilla työajan arvoilla. Kertoimen \(A\) kasvun voi siis tulkita teknologiseksi kehitykseksi.
Jos \(\alpha\) kasvaa, tuotos pienenee, kun if \(0 \lt h \lt 1\), ja kasvaa, kun \(h \gt 1\). Jos oletamme, että työajan \(h\) yksikkö on täsmälleen tunti, todennäköisesti \(h \gt 1\). Niinpä myös eksponentin \(\alpha\) kasvun voi tulkita teknologiseksi kehitykseksi.
Näitä kahta teknologisen kehityksen mallintamistapaa havainnollistaa kuvio 2. Vasemmassa kaaviossa kertoimen \(A\) kasvu kasvattaa tuotosta \(y\) samalla kertaluvulla kaikilla muuttujan \(h\) arvoilla. Jos esimerkiksi \(\alpha=\frac{1}{2}\) ja \(A\) kasvaa arvosta \(1\) arvoon \(2\), tuotos \(y\) kasvaa arvosta \(\sqrt{h}\) arvoon \(2\sqrt{h}\). Tuotos kasvaa toisin sanoen sata prosenttia kaikilla työajan arvoilla. Oikeanpuolisessa kaaviossa eksponentin \(\alpha\) kasvu kasvattaa tuotosta \(y\) kaikilla \(h\gt1\), kun \(A\) pysyy vakiona: jos esimerkiksi, \(A = 1\), \(h=8\) ja eksponentti \(\alpha\) kasvaa arvosta \(\frac{1}{3}\) arvoon \(\frac{1}{2}\), Angelan päivittäinen viljatuotos kasvaa \(2\) yksiköstä \(2\sqrt{2}\) yksikköön eli hieman yli 40 prosenttia.
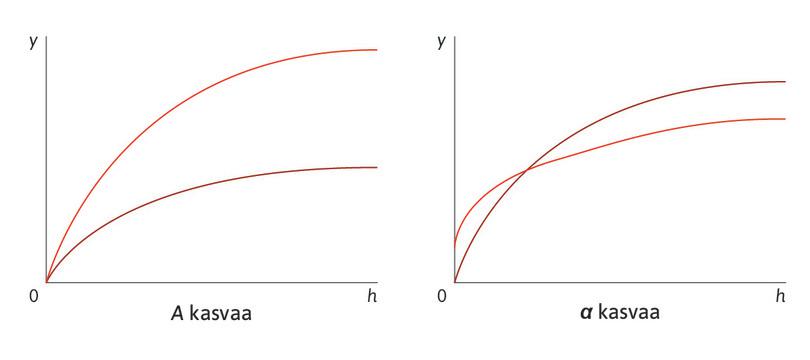
Kuvio 2 Tuotantofunktion siirtyminen: kaksi mallia.
Kaavioita vertaamalla voimme todeta, että kertoimen \(A\) muutos ja eksponentin \(\alpha\) muutos vaikuttavat samantyyppisesti mutteivät identtisesti. Eksponentti \(\alpha\) määrää funktion kuvaajan kaarevuuden. Kun \(\alpha\lt1\) oletuksemme mukaisesti, funktio on konkaavi. Jos \(\alpha=1\), funktio on suora; jos \(\alpha\gt1\), funktio on konveksi. Jos \(\alpha\) on pienempi kuin 1 ja kasvaa hieman, funktio muuttuu vähemmän konkaaviksi. Taloustieteellisesti muutos merkitsee, että Angelan lisätessä päivittäistä työaikaansa rajatuotos ei ala laskea yhtä nopeasti kuin pienemmillä eksponentin \(\alpha\) arvoilla.
Jos \(\alpha\) kasvaisi edelleen arvoon 1 ja sen yli, laskevan rajatuotoksen laki lakkaisi pätemästä. Sen vuoksi teknologisen kehityksen mallintamiseen eksponentin \(\alpha\) kasvuna liittyy perustavanlainen ongelma (sen pienemmän ongelman lisäksi, että työajan arvoilla \(h\lt1\) tuotos laskisi): teknologisen kehityksen aikakautta on kestänyt useampi vuosisata, mutta ihmisen työn rajatuotos on ja pysyy laskevana. On vaikeaa uskoa, että teknologinen kehitys vapauttaisi meidät konkaaveista tuotantofunktioista.
Ongelman voi välttää mallintamalla teknologista kehitystä kertoimen \(A\) muutoksena. Tällöin tuotos \(y\) kasvaa kaikilla työajan arvoilla \(h\gt0\), mutta tuotantofunktio pysyy konkaavina: rajatuotos on laskeva. Taloustieteilijät mallintavatkin teknologista muutosta yleensä eksponentin \(\alpha\) sijasta kertoimen \(A\) avulla.
Mallintaminen käy samaan tapaan mille tahansa tuotantofunktiolle. Oletetaan tuotantofunktio
\[y=Af(h),\]jossa \(f\) on mikä tahansa kasvava konkaavi funktio, jonka arvot ovat positiivisia kaikilla \(h\gt0\). Jos kerroin \(A\) kasvaa, tuotos kasvaa kaikilla muuttujan \(h\) arvoilla samassa suhteessa.
Myös tässä yleisemmässä tapauksessa laskevan rajatuotoksen ominaisuus säilyy. Työn rajatuotos on \(Af'(h)\). Jos työaika muuttuu arvosta \(h_0\) arvoon \(h_1\), työn rajatuotoksen suhteellinen muutos on
\[\frac{Af'(h_1) - Af'(h_0)}{Af'(h_0)} = \frac{f'(h_1) - f'(h_0)}{f'(h_0)}.\]Rajatuotos ei riipu kertoimesta \(A\). Siksi kertoimen \(A\) kasvu ei vaikuta siihen, miten paljon työn rajatuotos laskee suhteellisesti, kun työtuntien määrä kasvaa.
Lisälukemista: Malcolm Pemberton ja Nicholas Rau. 2015. Mathematics for economists: An introductory textbook, 4. painos (luvut 4.3 ja 7.3). Manchester: Manchester University Press.


