Leibniz 8.5.1 Kaupankäynnin hyödyt
Ostajat ja myyjät osallistuvat markkinoille, koska he hyötyvät siitä. Kaupankäynnin hyötyjä voi mitata kuluttajan ja tuottajan ylijäämällä. Näytämme, miten ylijäämä lasketaan matemaattisesti, ja osoitamme, että kilpailullisen tasapainon tuova allokaatio maksimoi kaupankäynnin hyödyt.
Esittelimme kuviossa 8.9a kaupankäynnin hyötyjä yhden kaupungin leipämarkkinoilla. Sama kaavio on kopioitu tähän kuvioksi 1. Kuluttajien ylijäämää edustaa kysyntäkäyrän alapuolelle ja markkinahinnan yläpuolelle jäävä ala. Tuottajan ylijäämä on tarjontakäyrän yläpuolella ja vaakasuoran hintasuoran alapuolella oleva ala. Alojen summa kuvaa kaupankäynnin kokonaishyötyjä näillä markkinoilla.
Hyötyjen matemaattista määritystä varten oletetaan, että leivän kysyntää kuvataan käänteisellä kysyntäfunktiolla \(P=f(Q)\), jossa \(P\) on hinta ja \(Q\) leipien määrä. Olettaen, että kysyntäkäyrät ovat kysynnän lain mukaisesti laskevia, \(f\) on laskeva funktio. Muista, että kysyntäfunktio ilmoittaa maksuhalukkuuden (WTP) leivästä. Jos kuluttajat järjestetään maksuhalukkuuden mukaiseen järjestykseen, \(q^{.}\). kuluttaja haluaa maksaa hinnan \(P = f(q)\). Ostaja, jonka maksuhalukkuus ylittää markkinahinnan, saa ylijäämää. Jos oletamme, että leivän markkinahinta on \(P_0\), \(q^{.}\). kuluttajan ylijäämä on \(f(q) - P_0\). Kaaviossa sitä vastaa kysyntäkäyrän ja hinnan pystysuora etäisyys määrän \(q\) kohdalla.
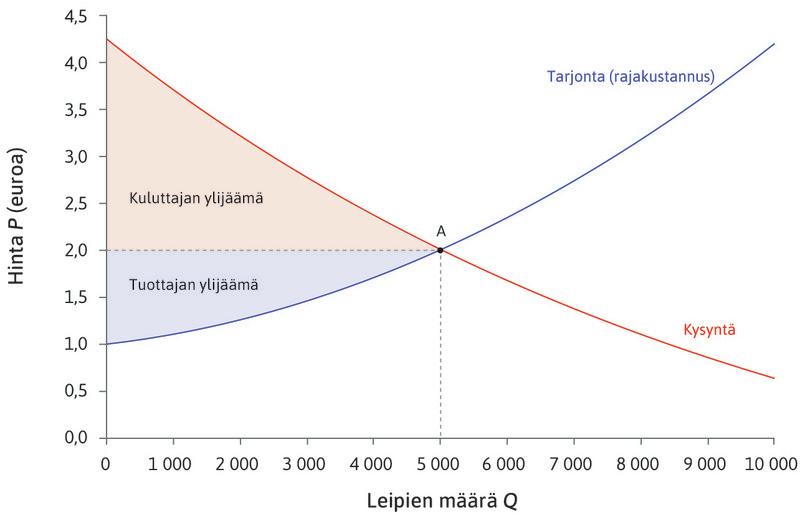
Kuvio 1 Leipämarkkinoiden tasapaino: kaupankäynnin hyödyt.
Kuluttajan ylijäämä saadaan lisäämällä yhteen kaikkien leivän tällä hinnalla ostavien kuluttajien ylijäämät. Koska olemme kuvanneet kysyntää jatkuvalla funktiolla (emmekä käsittele epäjatkuvia leipämääriä), lisäämme yksittäiset ylijäämät integroimalla. Oletetaan, että hinta on \(P_0\) ja myyty kokonaismäärä on \(Q\). Meidän on seuraavaksi laskettava yhteen ylijäämät \((f(q)-P_0)\) kaikissa kysyntäkäyrän pisteissä arvojen \(q=0\) ja \(q=Q\) välillä:
\[\mbox{kuluttajan ylijäämä} = \int_0^Q (f(q) - P_0) \, dq = \int_0^Q f(q) \, dq - P_0Q = F(Q) - P_0Q\]Lausekkeen merkintä \(F(Q)\) tarkoittaa funktion \(f\) määrättyä integraalia nollan ja \(Q\):n välillä. Se tarkoittaa määrien 0 ja \(Q\) välistä alaa kysyntäkäyrän alapuolella. Differentiaali- ja integraalilaskennan peruslauseen mukaan
\[F'(Q) = f(Q).\]Kysynnän laista seuraa, että \(F'\) on laskeva funktio, joten \(F\) on konkaavi funktio.
Punaisella merkitty ala kuviossa 1 kuvaa kuluttajan ylijäämää tilanteessa, jossa markkinat ovat kilpailullisessa tasapainotilassa, jossa hinta \(P_0 = 2\) ja määrä \(Q = 5~000\). Se on noin kolmion muotoinen ala, jota rajoittavat kysyntäkäyrä, pystyakseli ja vaakasuora viiva \(P=P_0\). (“Noin kolmion muotoinen” tarkoittaa, että ala olisi kolmio, jos kysyntäkäyrä olisi suora viiva.)
Voimme laskea tuottajan ylijäämän samalla tavalla. Muistanet Leibniz-osiosta 8.4.1, että käänteinen tarjontakäyrä on näiden markkinoiden leiväntuotannon rajakustannuskäyrä. Jos leipämäärän \(Q\) kokonaiskustannukset leipomoille ovat \(C(Q)\), rajakustannus on \(C'(Q)\) ja \(P=C'(Q)\) on käänteisen markkinoiden tarjontakäyrän yhtälö.
Oletamme, että niin kuin tekstissäkin, \(C'(Q)\) on positiivinen ja kasvaa määrän \(Q\) kasvaessa, mikä tarkoittaa, että \(C\) on kasvava konveksi funktio. Oletamme lisäksi, että \(C(0) = 0\), joten voimme kirjoittaa:
\[C(Q) = \int_0^Q C'(q) \, dq\]koska integrointi ja derivointi ovat toistensa käänteistoimituksia. Yhtälö kertoo, että kokonaiskustannus \(C(Q)\) on rajakustannuskäyrän alapuolinen ala, kun määrä on enintään \(Q\). Ellei \(C(0)\) olisi nolla, sanoisimme sen sijasta, että rajakustannuskäyrän alapuolinen ala on yhtä suuri kuin muuttuvat kokonaiskustannukset eli kokonaiskustannukset vähennettynä kiinteillä kustannuksilla, joita koituu, vaikkeivät leipomot tuota ollenkaan leipää.
Jos leipomo myy \(q\) leipää hintaan \(P_0\), sen ylijäämä on \(P_0\) vähennettynä leivän tuotantokustannuksella \(C'(q)\). Jos hinnalla \(P_0\) myytyjen leipien kokonaismäärä on \(Q\), tuottajan ylijäämä on kaikista leivistä saatujen ylijäämien summa:
\[\mbox{tuottajan ylijäämä} = \int_0^Q (P_0 - C'(q)) \, dq = P_0 Q - \int_0^Q C'(q) \, dq = P_0 Q - C(Q)\]Tästä lausekkeesta näkee, että kun oletuksemme mukaan \(C(0) = 0\), tuottajan ylijäämä on yhtä suuri kuin yrityksen voitto. Jos yrityksellä olisi myös kiinteitä kustannuksia, voitto olisi yhtä suuri kuin tuottajan ylijäämä vähennettynä kiinteillä kustannuksilla.
Kuvion 1 violetti ala kuvaa tuottajan ylijäämää kilpailullisessa tasapainotilassa, jossa \(P_0 = 2\) ja \(Q = 5~000\). Se on noin kolmion muotoinen ala, jota rajoittavat kysyntäkäyrä, pystyakseli ja vaakasuora viiva \(P=P_0\).
Huomaa, että kuluttajan ylijäämä \(F(Q)-P_0Q\) ja tuottajan ylijäämä \(P_0Q-C(Q)\) antavat kuluttajan ylijäämän arvon jokaiselle hinnan \(P_0\) arvolle ja jokaiselle määrän \(Q\) arvolle; ne pätevät riippumatta siitä, onko hinta markkinoiden tasapainohinta vai ei. Kuvio 2 kuvaa kuluttajan ja tuottajan ylijäämää yleisellä tasolla keinotekoisella hinnan \(P_0\) arvolla ja määrän \(Q\) arvolla.
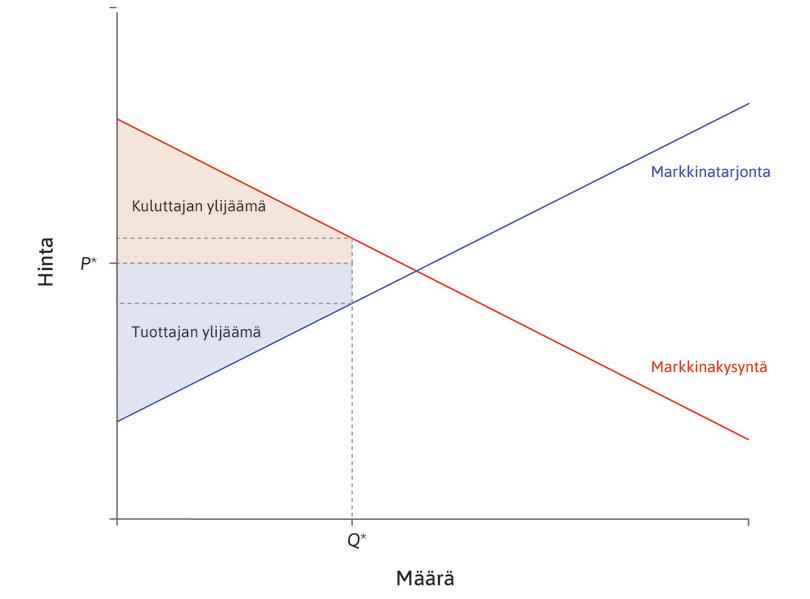
Kuvio 2 Kuluttajan ja tuottajan ylijäämä, kun hinta ja määrä eivät ole tasapainoarvossaan.
Kuluttajan ja tuottajan ylijäämän maksimointi
Koska kuluttajan ja tuottajan ylijäämä mittaavat kaupankäynnin hyötyjä, on hyödyllistä tietää, missä oloissa ne ovat suurimmillaan. Tarkastellaan ensin kuluttajan ylijäämää, josta käytämme merkintää \(CS\):
\[CS = F(Q) - P_0Q\]Tietyllä hinnan \(P_0\) arvolla kuluttajan ylijäämän maksimoiva määrän \(Q\) arvo saadaan asettamalla ylijäämän \(CS\) arvo nollaksi:
\[F'(Q) = P_0\]Huomaa, että koska \(F(Q)\) on konkaavi, ylijäämän \(CS\) toinen derivaatta on negatiivinen, mikä vahvistaa, että tämä ehto tuottaa maksimipisteen.
Tämä yhtälö kertoo, että jos hinta on \(P_0\), \(CS\) maksimoituu, kun myyty määrä on kysyntäkäyrällä hinnan \(P_0\) kohdalla eli kun kaikki kuluttajat, joiden maksuhalukkuus on vähintään \(P_0\), osallistuvat markkinoille. Jos kuluttajia on vähemmän, osa hyödyistä jää toteutumatta; jos jotkut muutkin kuluttajat ostavat leipää, he saavat negatiivisen ylijäämän, mikä vähentää kuluttajien kokonaisylijäämää.
Aivan samalla tavalla voidaan osoittaa, että tuottajan ylijäämä
\[PS = P_0Q-C(Q)\]maksimoituu, kun
\[P_0 =C'(Q).\]Olipa hinta mikä tahansa, tuottajat maksimoivat ylijäämänsä, jos leivän rajakustannus on yhtä suuri kuin hinta.
Kokonaisylijäämän maksimointi
Tuottajan ja kuluttajan ylijäämän summa on kokonaisylijäämä. Kun hinta on \(P_0\) ja myyntimäärä \(Q\),
\[N(Q) = F(Q) - P_0 Q + P_0 Q - C(Q)\] \[\text{kokonaisylijäämä} = \text{kuluttajan ylijäämä} +\text{tuottajan ylijäämä.}\]Kokonaisylijäämän voi esittää yksinkertaisesti:
\[N(Q) = F(Q) - C(Q)\]Huomaa, että kokonaisylijäämä riippuu vain myyntimäärästä. Olipa hinta mikä tahansa, leivästä maksettu summa on kuluttajien menetys ja yritysten samansuuruinen hyöty, joten ne kumoavat toisensa, kun arvioimme markkinoiden kokonaisylijäämää.
Saamme selville kokonaisylijäämän maksimoivan määrän \(Q^*\) asettamalla kokonaisylijäämän \(N(Q)\) derivaatan nollaksi. Silloin määrä \(Q^*\) toteuttaa yhtälön
\[F'(Q^*) =C'(Q^*).\]Varmistaaksemme, että määrä \(Q^*\) maksimoi kokonaisylijäämän \(N\), meidän on tarkasteltava toista derivaattaa. Muista, että \(F\) on konkaavi ja \(C\) konveksi. Siispä muuttujan \(F\) toinen derivaatta on negatiivinen ja muuttujan \(C\) toinen derivaatta positiivinen. Voimme päätellä, että kokonaisylijäämän \(N\) toinen derivaatta on negatiivinen, joten \(Q^*\) vastaa maksimipistettä.
Koska \(F'(Q^*) =f(Q^*),\) tämä yhtälö kertoo, että \(Q^*\) on pisteessä, jossa käänteinen kysyntäkäyrä \(P=f(Q)\) kohtaa käänteisen tarjontakäyrän \(P=C'(Q)\). \(Q^*\) on se tuotannon taso, jolla kysyntä- ja tarjontakäyrä leikkaavat. Tämä on tuotannon taso, kun markkinat ovat kilpailullisessa tasapainotilassa. Olemme siis osoittaneet, että kilpailullisen tasapainon allokaatiossa, jossa markkinoilla on tasapainohinta \(P^* = f(Q^*) =C'(Q^*)\), myyntimäärä maksimoi kaupankäynnin kokonaishyödyt.
Lisälukemista: Malcolm Pemberton ja Nicholas Rau. 2015. Mathematics for economists: An introductory textbook, 4. painos (luvut 8.4 ja 19.1). Manchester: Manchester University Press.


