Leibniz 3.4.1 Rajamuunnossuhde
Alexein opiskelupäätöksessä vaihtoehtoja rajaa vapaa-ajan ja arvosanan yhdistelmien mahdollisuuksien joukko. Alexein on siis tehtävä valinta: saadakseen hyvän arvosanan hänen on luovuttava osasta vapaa-aikaansa. Vapaa-ajan menetyksen ja arvosanan parannuksen yhteyttä mittaa rajamuunnossuhde. Tässä osiossa laskemme rajamuunnossuhteen tuotantofunktiosta.
Mahdollisuuksien rajan yhtälö
Kuvio 1 esittää Alexein mahdollisuuksien joukkoa. Käytimme mahdollisuuksien rajan piirtämiseen tuotantofunktiota, joka kuvasi tenttiarvosanan yhteyttä opiskeluun käytettyyn aikaan.
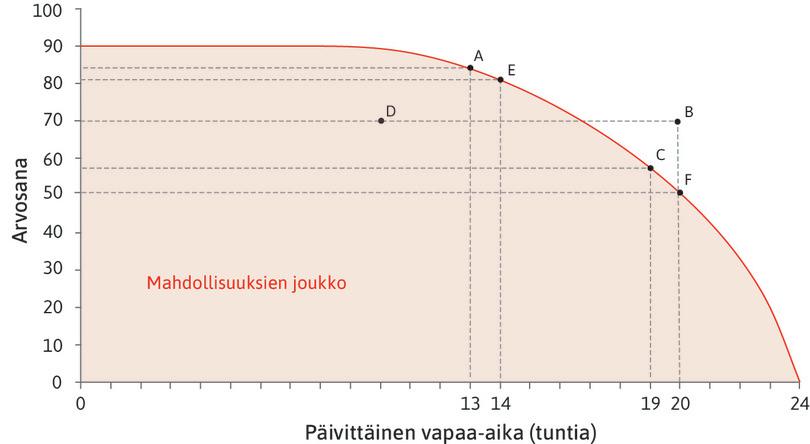
Kuvio 1 Miten Alexein valitsema vapaa-ajan määrä vaikuttaa arvosanaan?
Johdetaan mahdollisuuksien raja vielä matemaattisesti. Olkoon Alexein tuotantofunktio sama
\[y = f(h),\]jossa \(y\) on tuotos eli tenttiarvosana, \(h\) opiskeluun käytetty aika tunteina ja \(f\) kasvava funktio.
Mahdollisuuksien raja on arvosanan ja vapaa-ajan välinen yhteys. Jos Alexei pitää vapaata \(t\) tuntia, hänelle jää opiskeluaikaa
\[h=24-t.\]Sijoittamalla lausekkeen tuotantofunktioon saamme mahdollisuuksien rajan yhtälön:
\[y = f(24 - t)\]Rajamuunnossuhteen laskeminen
Totesimme graafisesti, että rajamuunnossuhde MRT on yhteydessä mahdollisuuksien rajan kulmakertoimeen. Kulmakerroin on mahdollisuuksien rajan yhtälön derivaatta. Jos Alexei pitää vapaata \(t\) tuntia, saamme selville hänen arvosanansa muutosnopeuden vapaa-ajan lisääntyessä soveltamalla yhdistetyn funktion derivointisääntöä eli derivoinnin ketjusääntöä:
\[\frac{dy}{dt} = f'(24-t)\frac{d}{dt}(24 -t)\]Sieventämällä saamme
\[\frac{dy}{dt} = - f'(24-t).\]Koska \(f\) on kasvava funktio, yhtälön oikea puoli on negatiivinen. Mahdollisuuksien raja on siis laskeva. Tämän näimme kuviosta. Mahdollisuuksien rajan kulmakerroin pisteessä \((t,\ f(24 -t))\) on negatiivinen luku \(-f'(24 -t)\).
- rajamuunnossuhde
- Se hyödykkeen määrä, josta päätöksentekijän on luovuttava saadakseen yhden yksikön lisää toista hyödykettä. Rajamuunnossuhde on mahdollisuuksien rajan kulmakerroin. Englanniksi marginal rate of transformation (MRT). Katso myös: rajasubstituutiosuhde.
Negatiivinen kulmakerroin merkitsee, että arvosana laskee vapaa-ajan lisääntyessä. Rajamuunnossuhde tarkoittaa nopeutta, jolla arvosana paranee Alexein vähentäessä vapaa-aikaansa. Se on kulmakertoimen itseisarvo eli positiivinen luku:
\[\text{MRT}=f'(24-t)\]Rajamuunnossuhteen tulkinta on seuraava: Jos vapaa-aika lisääntyy pienen määrän, vaikkapa \(\Delta t\) tuntia, tenttiarvosana heikkenee noin \(f'(24-t)\Delta t\) pistettä. Jos taas vapaa-aika vähenee \(\Delta t\) tuntia, tenttiarvosana paranee noin \(f'(24-t)\Delta t\) pistettä. Kuvio 2 esittää tuotantofunktiosta \(y=20,4h^{0,5}\) johdettua mahdollisuuksien rajaa. Sen muoto muistuttaa Alexein mahdollisuuksien rajaa. Tuotantofunktion alla on rajamuunnosuhteen kuvaaja. Se nousee siirryttäessä mahdollisuuksien rajaa pitkin oikealle, jolloin vapaa-aika lisääntyy ja tenttiarvosana laskee.
Rajamuunnossuhde kuvaa nopeutta, jolla Alexei joutuu luopumaan tenttipisteistä, jos hänen vapaa-aikansa lisääntyy. Se saadaan helposti tuotantofunktion derivaatasta. Koska opiskeluun käytetty tuntimäärä \(h\) on \(24 - t\), rajamuunnossuhde on sama kuin työn keskituotos \(f'(h)\). Rajamuunnossuhde kasvaa siirryttäessä mahdollisuuksien rajaa pitkin kohti suurempaa vapaa-ajan määrää ja pienempää opiskeluun käytettyä tuntimäärää. Tämä johtuu työn laskevasta rajatuotoksesta: koska \(f'(h)\) on muuttujan \(h\) laskeva funktio, \(f'(h)\) kasvaa muuttujan \(h\) arvon pienetessä.
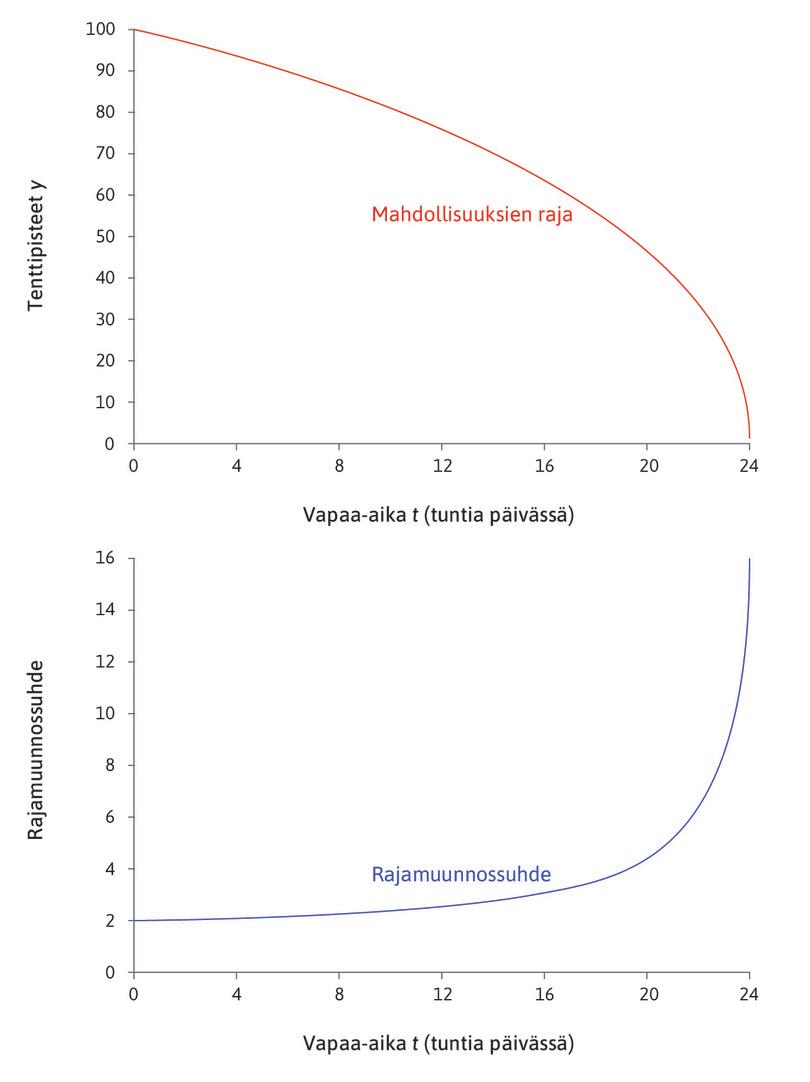
Kuvio 2 Mahdollisuuksien raja \(y = 20,4(24-t)^{0,5}\) ja sitä vastaava rajamuunnossuhde.


