Leibniz 8.4.1 Markkinoiden tarjontakäyrä
Monien pienten leipomoiden ja monien kuluttajien mallissamme jokainen leipomo on leipämarkkinoilla hinnanottaja. Yhden leipomon tarjontakäyrä riippuu sen rajakustannuskäyrästä. Markkinoiden tarjonta tietyllä hinnalla on leivän kokonaismäärä, jonka kaikki leipomot yhdessä tarjoavat. Tässä Leibniz-osiossa selitetään, miten yrityksen ja markkinoiden tarjontakäyrät selvitetään matemaattisesti.
Oletetaan, että kaupungissa on \(m\) leipomoa ja leipomon \(i^{.}\) kokonaiskustannusfunktio on \(C_i(Q_i)\), jossa \(Q_i\) on sen tuottamien leipien määrä, kun \(i = 1,\ …,\ m\). Kaikki leipomot ovat hinnanottajia. Määrittelemme ensin yksittäisten leipomoiden tarjontafunktiot ja laskemme ne sitten yhteen markkinoiden tarjontakäyräksi.
Leipomon i tarjontafunktio
Leipomo \(i\) pitää markkinahintaa \(P\) annettuna ja valitsee määrän \(Q_i\) maksimoidakseen voittonsa:
\[\Pi_i = PQ_i-C_i(Q_i)\]Voittofunktion derivointi muuttujan \(Q_i\) suhteen ja derivaatan asettaminen nollaksi antaa ensimmäisen kertaluvun ehdon:
\[P = C_i'(Q_i)\]Sen voi tulkita seuraavasti: yritys valitsee määrän niin, että rajakustannus on yhtä suuri kuin markkinahinta. Jokaista hinnan \(P\) mahdollista arvoa vastaa optimaalinen määrä \(Q_i\), joka toteuttaa tämän yhtälön. Koska yhtälö kertoo hinnan \(P\) arvon, jolla yritys tarjoaa määrän \(Q_i\), sitä voi kuvata yrityksen käänteiseksi tarjontafunktioksi. Tekstin kuvio 8.7, joka on kopioitu tähän kuvioksi 1, osoittaa yrityksen rajakustannuksen tai yhtäpitävästi sen käänteisen tarjontafunktion \(P = C_i'(Q_i)\) kaavion vasemmalla puolella.
Tämän funktion käänteisfunktio on suora tarjontafunktio. Se kertoo määrän \(Q_i\) arvon, jonka yritys valitsee, kun hinnalla of \(P\) on tietty arvo. Kirjoitamme yrityksen tarjontafunktion muotoon
\[Q_i = Q_i^S(P)\]Oletetaan, että yrityksen \(i\) kustannusfunktio on \(C_i(Q_i) = 3 Q_i^2+2Q_i\). Rajakustannuksen laskemalla saamme tietää, että sen käänteinen tarjontafunktio on \(P = 6 Q_i+2\). Järjestelemällä termit saadaksemme tietää määrän \(Q_i\) hinnan \(P\) suhteen saamme tarjontafunktion \(Q_i^S(P) = (P-2)/6\).
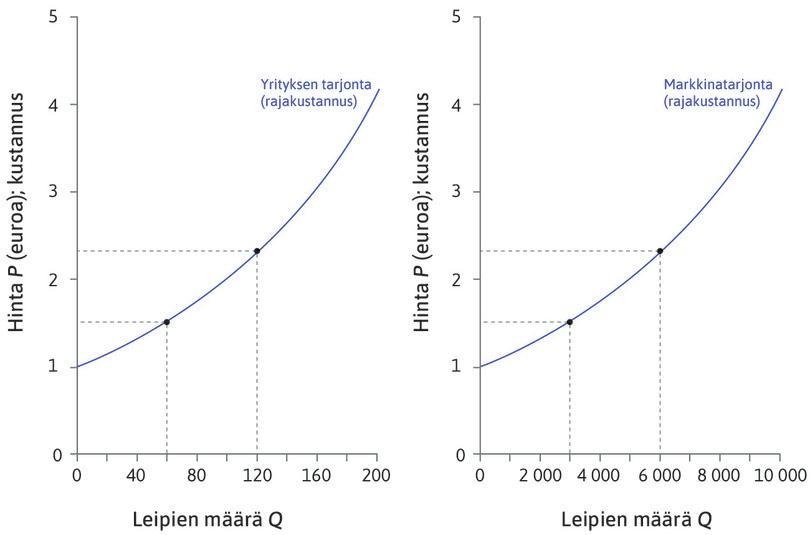
Kuvio 1 Markkinoiden tarjontakäyrä.
Markkinoiden tarjontafunktio
Kun markkinahinta on \(P,\ Q_1^S (P),\ Q_2^S (P),\ \ldots,\ Q_m^S (P)\) ovat \(m\) yrityksen tarjoamia määriä. Jos kaikilla yrityksillä olisi sama kustannusfunktio, niillä olisi identtinen tarjontafunktio; jos ei, tarjontafunktiot ovat erilaisia. Koko markkinoille tarjottava määrä hinnalla \(P\) on
\[Q^S(P) = \sum_{i = 1}^m Q_i^S (P).\]Funktio \(Q^S(P)\) on markkinoiden tarjontafunktio. Funktion kaavio on markkinoiden tarjontakaavio, jossa on tavallisesti hinta \(P\) pystyakselilla ja määrä \(Q\) vaaka-akselilla. Graafisesti siirtymistä yksittäisten yritysten tarjontakäyristä koko markkinoiden tarjontakäyrään voi tarkastella yhteenlaskuna vaaka-akselia pitkin: lasketaan yhteen yksittäisten yritysten tarjonta kullakin hinnalla ja saadaan tulokseksi markkinoiden tarjonta. Kuvion 1 oikeanpuoleiseen osaan on piirretty markkinoiden tarjonta olettaen, että markkinoilla on 50 leipomoa (\(m = 50\)), joilla on identtiset tarjontafunktiot. Kullakin hinnalla markkinoiden tarjonta \(Q^S(P)\) on 50 kertaa yksittäisen yrityksen tarjonta \(Q_i^S(P)\).
Kuten tekstissä todetaan, markkinoiden tarjontakäyrän voi tulkita koko markkinoiden rajakustannuskäyräksi. Se on minimihinta, jolla myyjät ovat valmiita tarjoamaan tietyn määrän hyödykettä. Koska jokainen yritys valitsee tuotannon tason niin, että hinta on yhtä suuri kuin rajakustannus, jokaisella leipiä tuottavalla on oltava sama rajakustannus. Markkinoiden tarjontakäyrä mittaa kokonaistuotannon ja tämän tuotantomäärän yhteisen rajakustannuksen suhdetta. Markkinoiden tarjontakäyrän tulkinta rajakustannuskäyräksi on yksi syy siihen, että tarjontakäyrät piirretään tavallisesti niin, että hinta \(P\) on pystyakselilla.
Lisälukemista: Malcolm Pemberton ja Nicholas Rau. 2015. Mathematics for economists: An introductory textbook, 4. painos (luku 7.4). Manchester: Manchester University Press.


