Leibniz 2.7.1 Tuotantofunktio
Maatalousvaltaisen talouden mallimme tuotantofunktio kuvaa, miten viljan tuotanto riippuu työpanoksesta eli viljelijöiden lukumäärästä. Tässä osiossa esitämme tuotantofunktion matemaattisesti ja kuvaamme sen ominaisuuksia.
Viljan tuotantofunktio näkyy kuviossa 1.
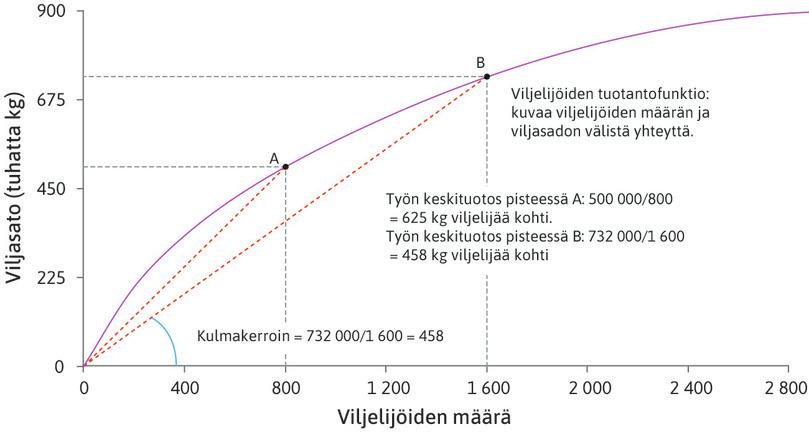
Kuvio 1 Viljelijöiden tuotantofunktio: työn laskeva keskituotos
Jos \(x\) on työpanos eli viljelijöiden määrä ja \(y\) viljan kokonaistuotanto kiloina, voimme kirjoittaa tuotantofunktion muotoon
\[y=f(x).\]\(f(.)\) voisi olla mikä tahansa funktio, mutta jos sen on määrä edustaa kuvion kaltaista tuotantofunktiota, sillä on oltava tiettyjä ominaisuuksia. Ensiksi näemme, että jos panos on nolla, viljaa ei tuoteta lainkaan. Jos panos on suurempi kuin nolla, viljan kokonaistuotanto on aidosti positiivinen:
\[f(0)=0, \quad f(x)>0 \text{ if } x>0.\]Toiseksi funktio on kasvava: kun \(x\) kasvaa, myös \(y\) kasvaa. Siispä sen kulmakerroin eli funktion derivaatta on positiivinen. Voimme kirjoittaa:
\[\frac{dy}{dx}>0\]tai yhtäpitävästi:
\[f'(x)>0.\]Nämä kaksi ominaisuutta ovat tyypillisiä useimmille tuotantofunktioille. Kuvion tuotantofunktiolla on myös se ominaisuus, että se loivenee sitä mukaa kuin \(x\) kasvaa. Toisin sanoen sen kulmakerroin \(\frac{dy}{dx}\) laskee, kun \(x\) kasvaa. Se tarkoittaa, että sen toinen derivaatta on negatiivinen:
\[\frac{d}{dx}\left(\frac{dy}{dx}\right)=\frac{d^2y}{dx^2}<0\]tai yhtäpitävästi:
\[f''(x)<0.\]Lisälukemista: Malcolm Pemberton ja Nicholas Rau. 2015. Mathematics for economists: An introductory textbook, 4. painos (luvut 7.3, etenkin sivu 127, ja 8.2). Manchester: Manchester University Press.


